BESACE
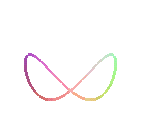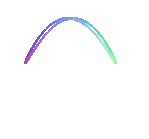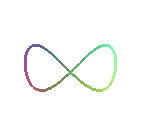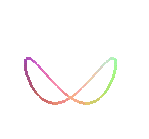
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BESACE
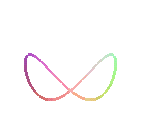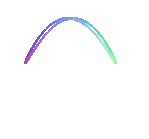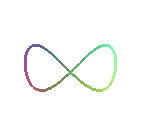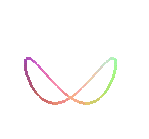
| Curve studied and named by Cramer in 1750. |
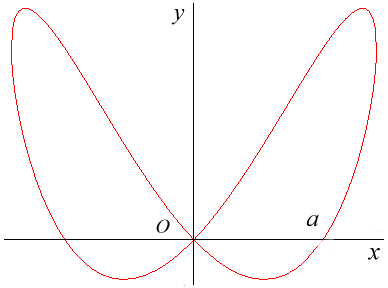 |
Cartesian equation:
Or
of Rational
quartic.
|
Given a diameter [AB] and a point O on a circle (C), the associated besace is the locus of the points M on a moving line (D) parallel to (OA) such that QM=OP where P is an intersection point between (D) and (C) and Q is the projection of O on (D) (here, A(a,0) and B(0,b)).
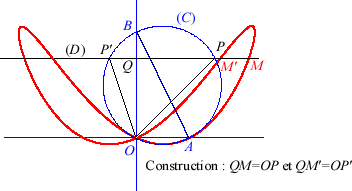
The third form of the Cartesian equation shows that besaces
are the polyzomal curves median
of the coaxial parabolas
and
.
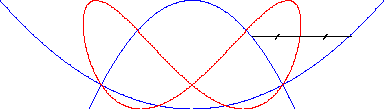
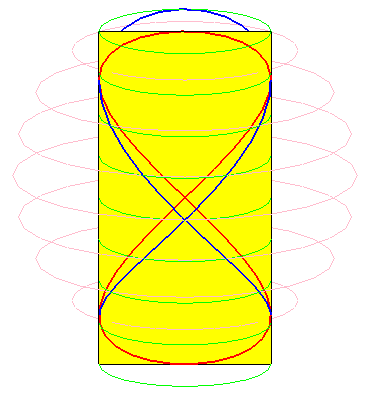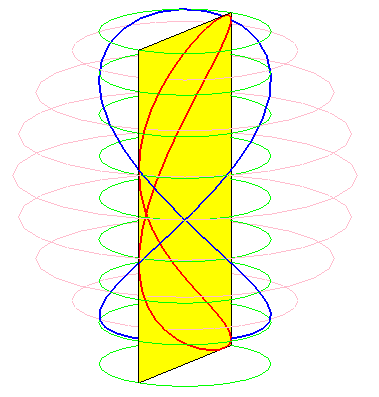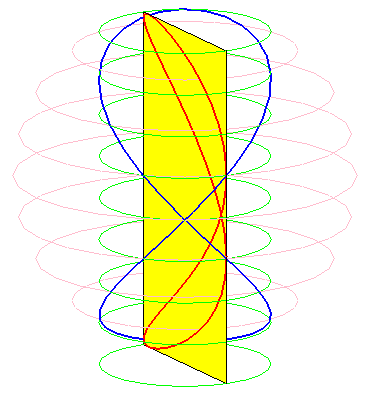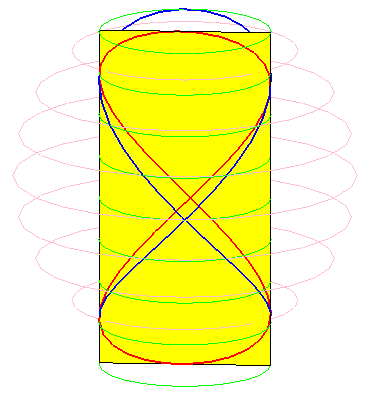
Besaces are the projections of Viviani's curve on the planes passing by the axis of the cylinder on which the curve is traced.
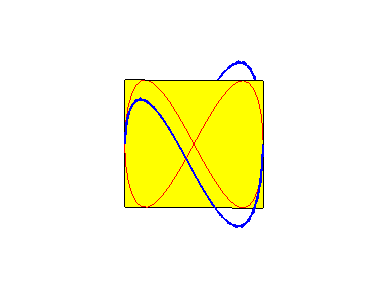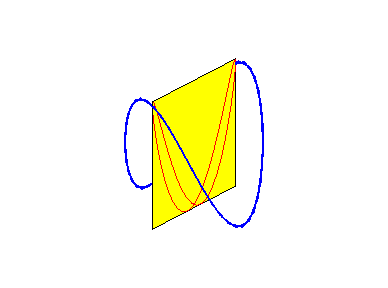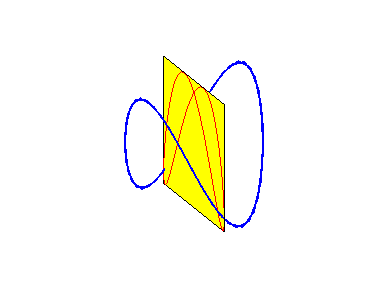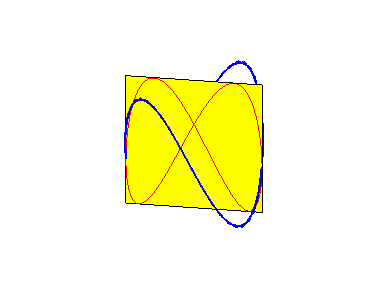
When b = 0 (i.e. when the circle is tangent to
Oy), we have the lemniscate of Gerono
and when a = 0, a parabolic segment.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017