Regular bifolium

REGULAR BIFOLIUM

Origins: see bifolium.

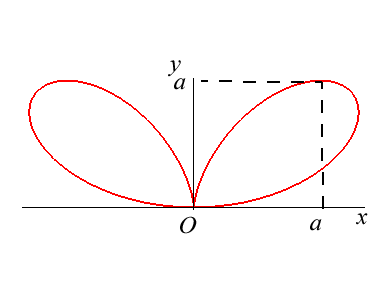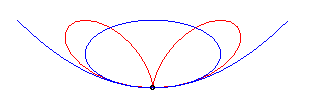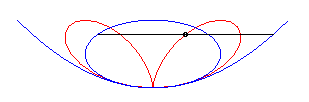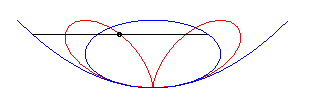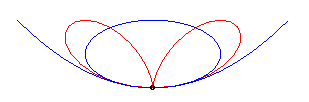
Polar equation:

(or

in a frame rotated by p/2).
Cartesian equation:

.
Cartesian parametrizations:

where

;

where

;

where

;

where

and

.
Total area:

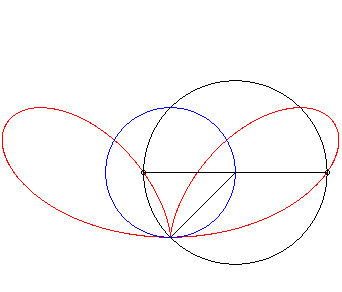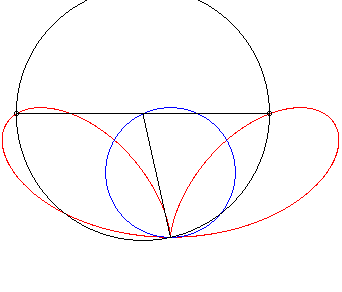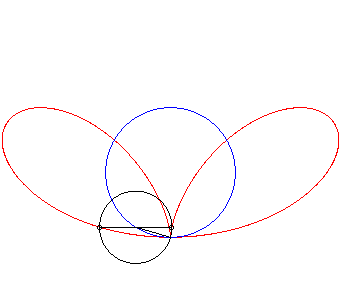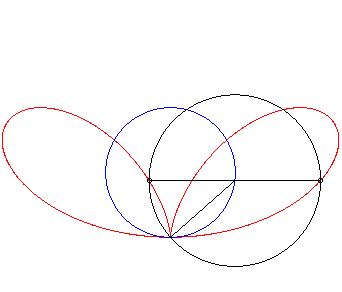
Given a variable point N on a circle of diameter [OA] (here A(0,a)), the regular bifolium is the locus of the points M on the perpendicular to (OA) passing through N for which NM = ON. In other words, the regular bifolium is a strophoidal curve of a circle, with a pole O on the circle and a point A at infinity in the direction of the tangent to the circle at O.
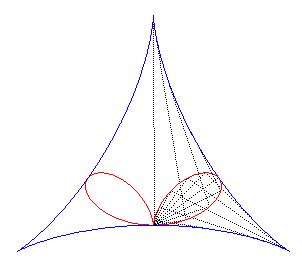
The Cartesian equation shows that the regular bifolium is the polyzomal curve medial between the parabola and the ellipse .
The regular bifolium also is the pedal of the deltoid with respect to one of its vertices (see at folium).
It is also a plane projection of Viviani's curve.

It can also be obtained as the orthopolar of a circle.

See also fish curves and compare with the double heart curve and the pedal of the tractrix.

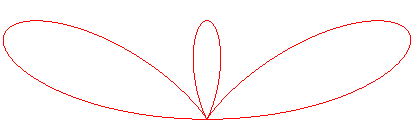
Variation:
Adding to adds a lobe.... More generally, yields an n-folium.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

Variation:	Adding to adds a lobe....	More generally, yields an n-folium.