Homemade name, stemming from the fact that Brocard defined an original curve using this transformation (see multicardioid). Other name: fan transformation.

 

Equation of the initial curve		with f -periodic with respect to .
Equation of the Brocard transformation

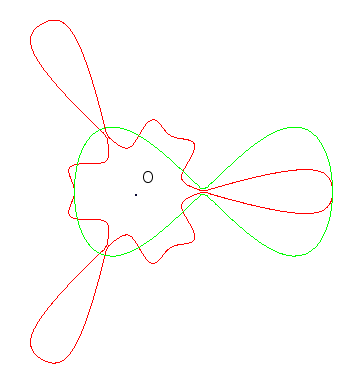
The Brocard transformation of centre O and parameter n is defined by the above formulas.
 
 

For n  > 0, the points on the initial curve (in green, opposite) have their polar angle divided by n, and the curve obtained is duplicated by consecutive rotations by 360/n °. If n is an integer, then the curve obtained is invariant under rotations by 360/n °. Therefore, it is a Goursat curve if the initial curve also has an axis symmetry and if O is on this axis.

Examples:
 

Initial curve	pole	Brocard transformation
straight line	outside of the line	knots
circle	on the circle	roses
Pascal's limaçon	pole of the limaçon	conchoids of a rose
conic	focal point of the conic	polygasteroids
kappa curve	centre of the kappa	Cotes' spirals
cardioid	any point	multicardioids

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017