| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CARTESIAN CURVE
| René Descartes (1596-1650): French philosopher, mathematician and physicist. |
Reduced Cartesian equation:  .
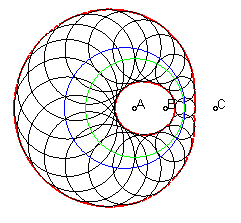
If 
then the equation can be written:
and a cyclic generation stems from the circle with centre
O and radius R as the initial curve, the circle with centre
A(a,0) and radius In the frame (A, |
The Cartesian curves are the bicircular
quartics with two cusps at infinity.
They are the curves that can be defined as cyclic
curves with a circle as the initial curve (called initial circle).
In other words, they are the envelopes of the circles whose centres describe
the initial circle and such that a fixed point has a constant power with
respect to these circles.
When p < 0, we get the genuine complete Cartesian
oval (???).
, 
=
radius of the inversion circle:
), the
curve does not have real points.
or 
and 
)
we get, twice, the genuine complete Cartesian ovals again.
),
we get the special Cartesian curves, that have a tripolar equation: 
with ??. These curves are inverses of Cartesian ovals.
, 
or r = 0), we get a limaçon
of Pascal.
To sum up, the family of Cartesian curves is composed
of complete Cartesian ovals and their inverses.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
as inversion circle, and inversion power p.
, 
):
.
.