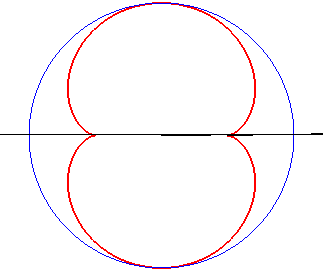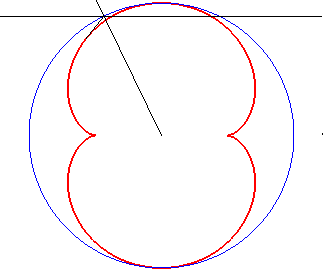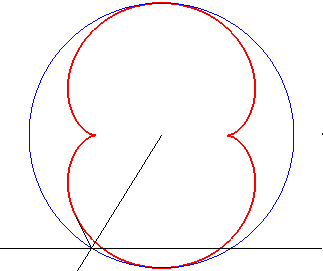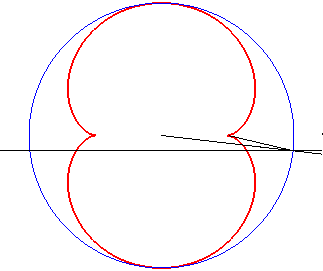
When the light source is on the circle (a = b), we get the cardioid:
When the light source is at infinity (b =
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CAUSTIC OF A CIRCLE
1) Caustic by reflection of a circle:
| Cartesian parametrization: When the light source is on the circle (a = b), we get the cardioid: When the light source is at infinity (b = |
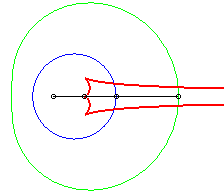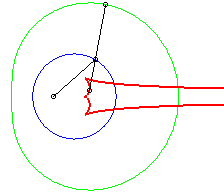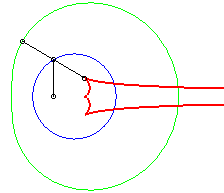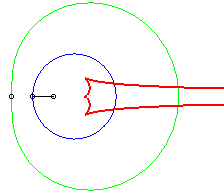
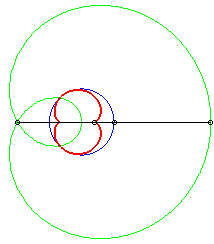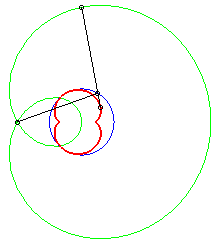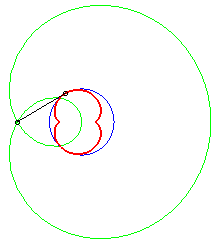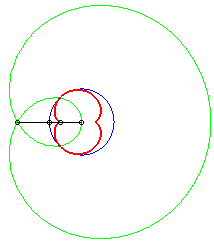
The caustics by reflection of circles are the envelopes of the reflection of rays, emitted by a light source placed at finite or infinite distance, by a circle.
According to the properties of caustics, they are the evolutes of the orthotomics of circles, thus the evolutes of Pascal's limaçons.
In the pictures below, the circle is in blue, the limaçon
in green and the caustic in red.
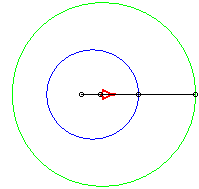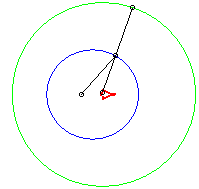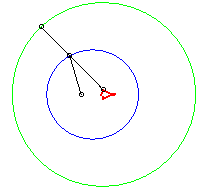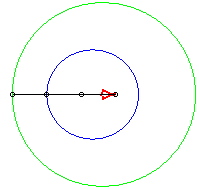
light source placed at (b,0) where b = - a / 4 |
b = - a / 2 |
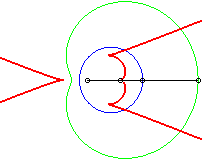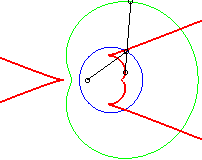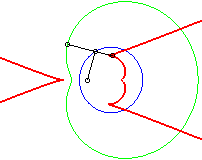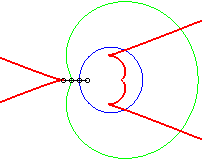
b = - 3a / 4 |
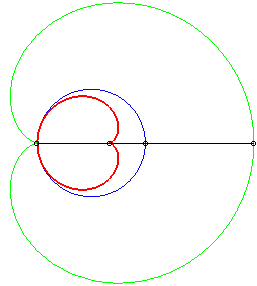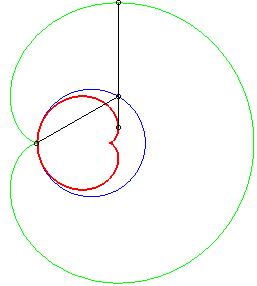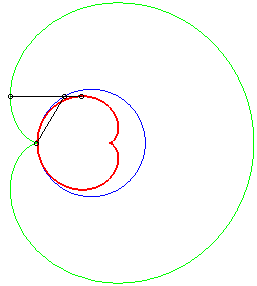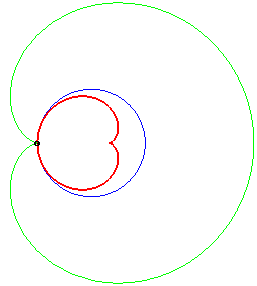
b = - a: case of the cardioid |
b = - 2a |
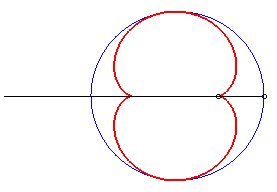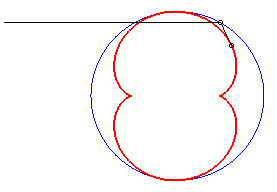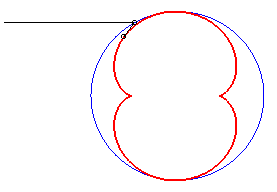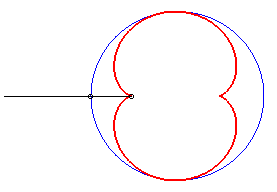
|
The caustics of circles can be obtained as sections of caustic surfaces of circular cones for rays at infinity (the case of the nephroid being obtained for a cylinder).
This property is the reason why we can see these curves in a conical container full of liquid illuminated by a light beam.

2) Caustic by complete refraction of a circle, light source
at infinity.
| Cartesian parametrization: Opposite, the case n = 2. |
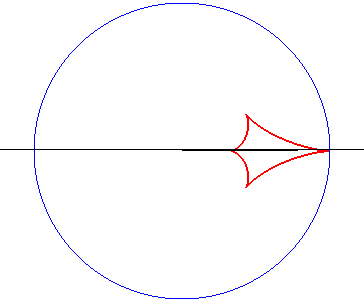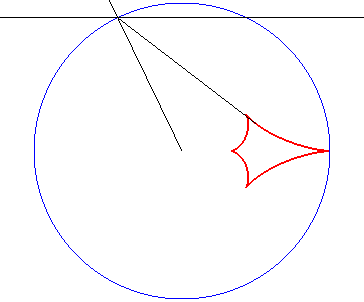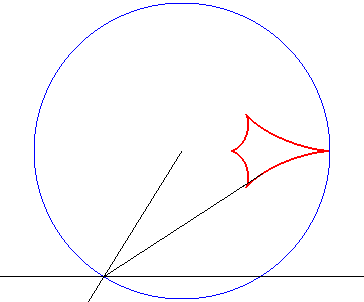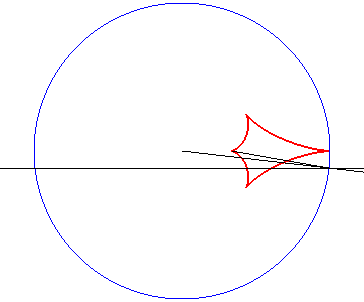 |
| When n goes to 1, the previous curve goes to |
 |
The case of a light source at finite distance is treated
on this page.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017