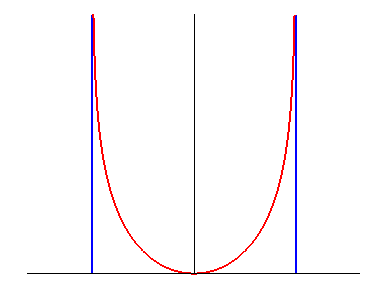
The catenary of equal strength differs from the classic catenary in its two asymptotes.

Differential equation: . Cartesian equation: . Curvilinear abscissa: (reminder: sec = 1/cos) Cartesian tangential angle: . Radius of curvature: . Intrinsic equation 1: . Intrinsic equation 2:. Area delimited by the curve, Ox, and the asymptotes: . Transcendental curve.

The catenary of equal strength is the shape taken by an inextensible flexible massive wire hanging from two points, when the linear mass density (i.e., in practical terms, the width of the wire) is proportional to the tension.
Such a wire is not more likely to break in any point than in another.
This curve, upside-down, represents the profile of a vault without overload (Brocard) ??
 
 

With the notations of the opposite figure ( = tension of the wire at M, m = linear mass density of the wire), we write that the sum of the forces at M is zero: . This simplifies to , which, by integration, gives . We derive from this that  and  hence  and, as we want,  so that , and we get the differential equation  that yields the Cartesian equation above.

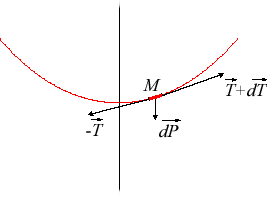The linear mass density is then equal to , which sets the width of such a wire.

The formula  shows that the projection of the segment radius of curvature on the x axis has constant length; this property is a characteristic of the catenary of equal strength.
 
 

The catenary of equal strength is also the special case k = 1 of the family of curves with intrinsic equation 1 . Such curves do not have a known name but their parametrization is:  Opposite, an animation for k ranging from 0 to 6, with stops at k =1 (catenary of equal strength), k = 2 (syntractrix), and k = 4.

See also Ribaucour curve, of which the catenary of equal strength can be considered to be a special case.

The radial curve of the catenary of equal strength is the line x = a and its Mannheim curve is a catenary.
 
 

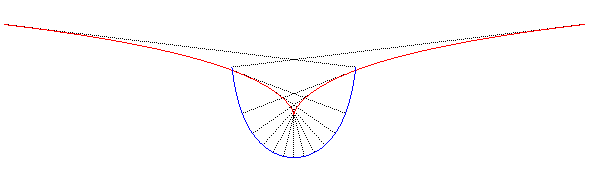
The evolute of the catenary of equal strength is the curve with parametrization:

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017