From the Greek Kissos: ivy.

 

Polar equation: . Cartesian equation: . Rational circular cubic with a cuspidal point. Rational Cartesian parametrization: . Coordinates of the intersection point with the asymptote: . Coordinates of the point with maximal abscissa: .

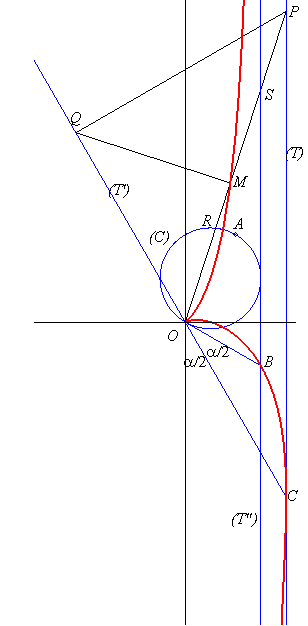
The simplest construction of a cissoid is by double projection: given two lines (T) and (T') and a point O on (T'), a variable point P on (T) is projected on the point Q on (T'), which in turn is projected on M on (OP): the cissoid is the locus of M (see the figure above); the cissoid of Diocles is obtained when (T) and (T') are strictly parallel.
Here, (T) is the vertical line: x = a, (T') is the line , forming an angle of  with the latter.

But the classical construction of the cissoid is... cissoidal: given a circle (C), a point O on this circle and a tangent (T") of this circle, a variable point S on (T") defines a point R at the intersection between (OS) and (C): the cissoid is the locus of the points M such that.

The cissoids are therefore the cissoids with pole O of a circle  (C') passing through O and of the symmetrical image (T') of a tangent to (C') with respect to O; here, (C') is the symmetrical image with respect to O of the circle (C) with polar equation:  and (T") is the line: .
 

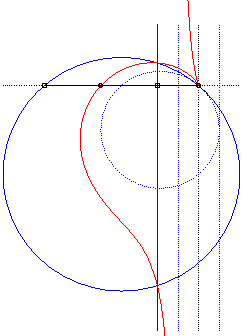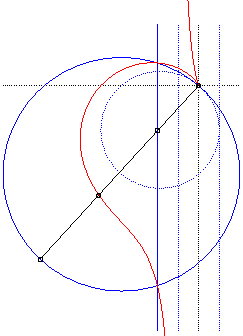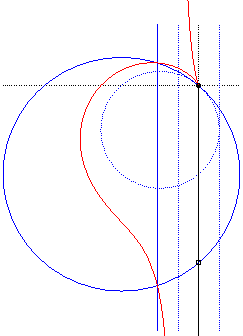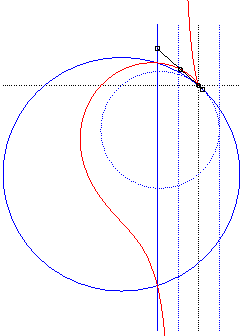Here, the circle (C') is dotted, the full circle being its image by the homothety with centre O and ratio 2. The dotted line (T) is on the left, when the full line is its image by the same homothety. The cissoid is then the median curve with centre O of these circle and line.

Cissoids can be defined algebraically as cuspidal (i.e. with a cuspidal point) circular cubics.
As can all rational circular cubics, the cissoid can also be defined as:
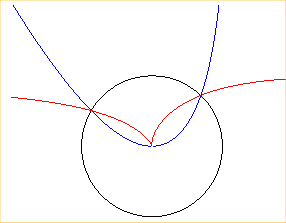
     - the pedal of a parabola with respect to one of its points (here the parabola with focus A and tangent at the vertex  ).

 - the inverse of a parabola with respect to one of its points (here, the parabola , the circle of inversion being the circle (O, a)).

© Robert FERRÉOL 2017