Conchoid

CONCHOID

From the Greek Kogkhoeidês: similar to a shell.
Other name: conchoidal curve.

Polar equation:

where

is the polar equation of the initial curve.

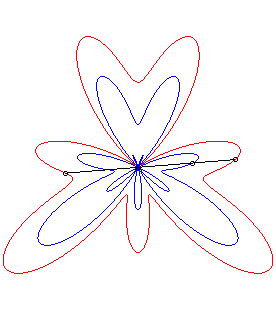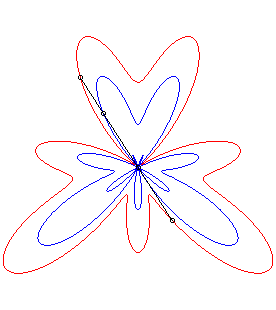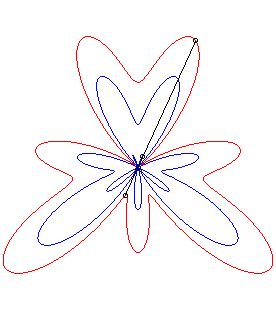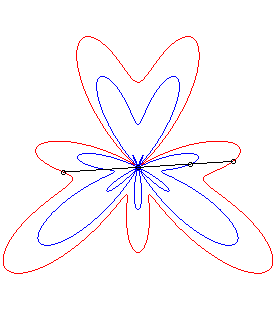
The conchoid of a curve

with pole O (or with respect to O) and modulus a (algebraic value) is the locus of the points M on the line (OM₀) such that

, when M₀ describes

.
For example, the curve described by a dog pulling on its leash of length a in the direction of a cat located at O, when its master describes the curve

, is the conchoid of this curve, with modulus –a.

Or, consider a rigid bar sliding along a point O with one of its points constrained to describe the curve : all the points on the bar describe conchoids of . The general notion at play here is the glissette.

Conchoids can also be physically obtained by a cylindrical anamorphosis.

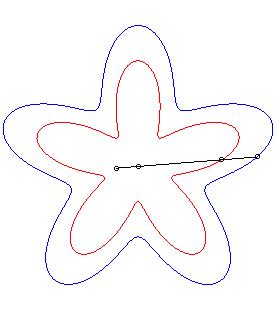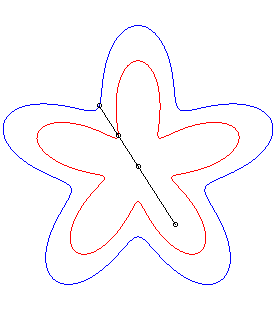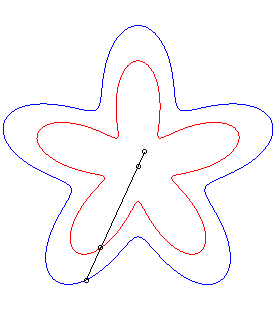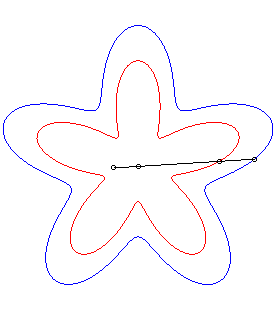This notion is also a special case of the cissoid.

Examples:
    - conchoids of lines, or conchoids of Nicomedes.
    - conchoids of circles, including the limaçons of Pascal when the pole is on the circle.
    - conchoids of roses.
    - conchoids of right strophoids with respect to the summit of the loop are strophoids.
    - conchoids of the Archimedean spiral with respect to its centre are isometric Archimedean spirals.
    - conchoids of conics with respect to their focus, or Jerabek's curves.

Dürer's conchoids are of another kind.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra