CONCHOID OF NICOMEDES
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CONCHOID OF NICOMEDES
| From the Greek Kogkhoeidês: similar to a
shell.
Nicomedes (2nd century BC): Greek mathematician. |
Polar equation: 
.
Cartesian equation: 
or  .
Rational Cartesian parametrization: 
(with 
).
Rational circular quartic. |
The conchoids of Nicomedes are the conchoids of straight lines (here, the line is (D) and its equation is x = a; b can be considered to be positive without loss of generality).
They have two infinite branches for which the line (D)
is an asymptote, the left one being ordinary for 0 < b < a,
with a cuspidal point for b = a and with a loop for b > a.
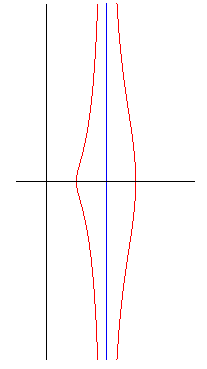
0 < b < a |
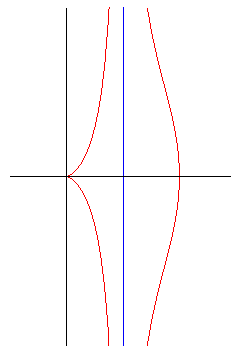
a = b |
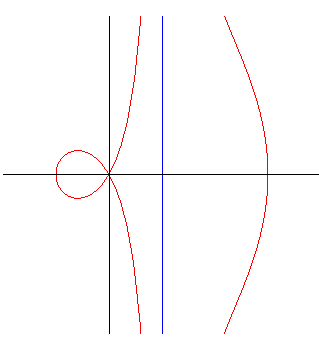
b > a |
The conchoids of Nicomedes are also the cissoids
of the circle with centre O and radius b and the line (D)
with respect to the centre of the circle.
The conchoids of Nicomedes are the trisectrix.
Opposite, we see the trisecting of an angle of 30° ( );
note that to each angle 
to be trisected corresponds a different conchoid ( ).
Method: draw a triangle OHI with a right angle in H, such that OIH is the angle to trisect. Draw the conchoid of the line (IH) with pole O and modulus OI. The circle with centre I and radius OI cuts the conchoid at M, symmetrical image of O about I and a second point N, the construction of which can only be approximative. The trisected angle is NIJ. |
 |
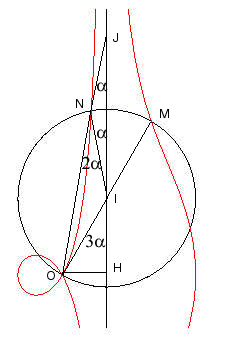For b = 2a, the conchoid of Nicomedes is also a duplicatrix (see [GomesTexeira] page 266, or [Carrega] page 72).
One can also take an interest, more generally, to the
movement
of a plane over a fixed plane, called linear conchoidal movement,
the moving plane being linked to the line (O
),describing
the line (D) (and
being fixed in the moving plane): indeed, the conchoids of Nicomedes are
the roulettes of this movement, for tracing points located on the line
(O).
With the notations of this
page, we have: 
.
Therefore, in the frame centred on (a, 0), the
base
is the parabola:
,
the rolling curve the Kampyle
of Eudoxus with polar equation 
and the roulettes are the curves: 
which give conchoids for 
.
 |
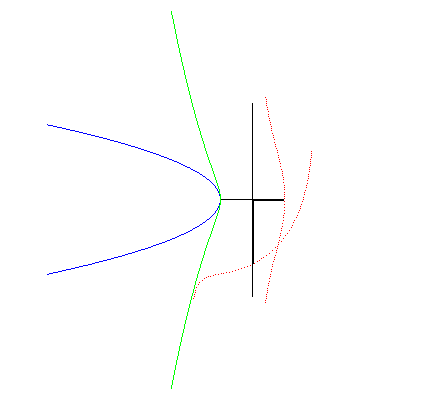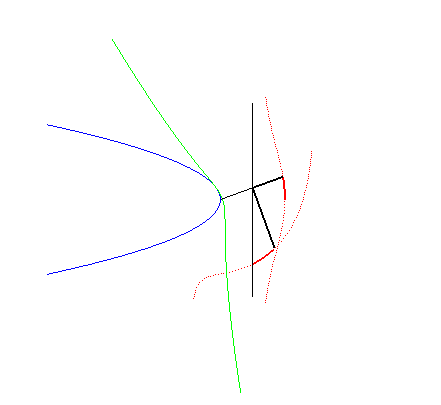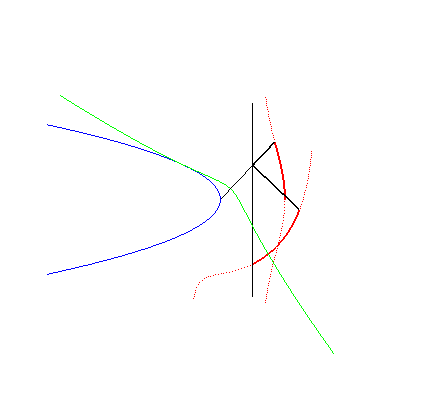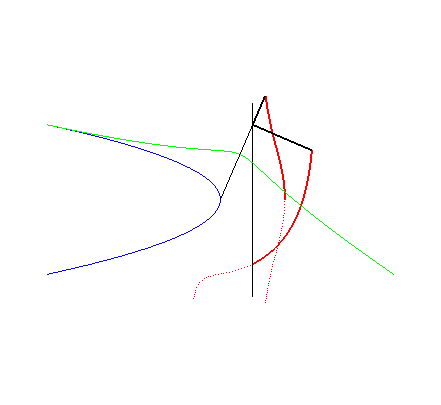Therefore, the conchoids of straight lines are the loci
of points on the transerval axis of a Kampyle rolling without sliding on
a parabola.
The other roulettes of this movement are the loci of the
point M forming a constant angle Opposite are drawn a conchoid of a line and another roulette,
obtained for |
The movement obtained when swapping the base and the rolling
curve is the Kappa.
 See here the reason why portions of conchoids of Nicomedes appear in a conical anamorphosis. |
|
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2017
when 
;
the latter curve was named "orthoconchoid of a line" by Neuberg in 1904,
and any roulette could be called "isoconchoid of a line".
