Crosscurve

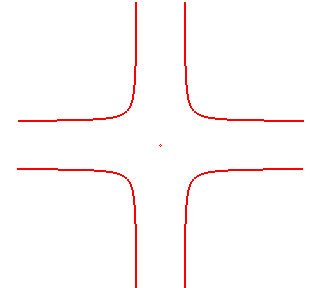
CROSSCURVE

Curve studied by Terquem in 1847 and Schoute in 1883.
Other name: policeman on point-duty curve

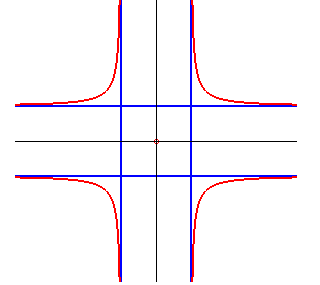The origin is an isolated point of the algebraic curve "forgotten" by the parametrization. Cartesian equation: (special case of Lamé curve) or , or , or even .
Cartesian parametrization: .
Polar equation when a = b (rectangular crosscurve): (special case of Cotes' spiral).
Rational quartic.

The crosscurve is the image of the ellipse by a biaxial inversion (with axes the axes of the ellipse) defined here by: . The four asymptotes are tangent to the initial ellipse at its summits.

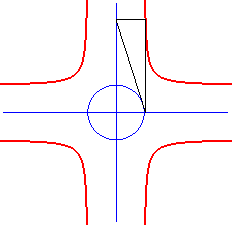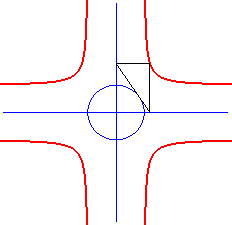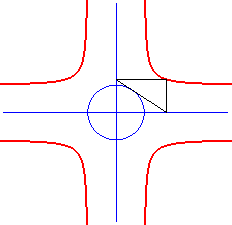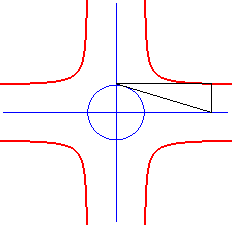
It can be geometrically obtained as the locus of the intersection points between the two lines parallel to the axes and passing by the intersection points between one of the tangents of the ellipse and the axes.
Therefore, the crosscurve is to the ellipse what the bullet-nose curve is to the hyperbola.

The rectangular crosscurve is also the locus of the focus of a parabola constrained to remain tangent to two perpendicular axes; it is therefore a glissette.
For a parabola with parameter p, we get a crosscurve with parameters a = b = p/2.
In this movement, the locus of the vertex of the parabola (in green, opposite) is the curve with parametrization: (), and equation .

Finally, the rectangular crosscurve is the planar section of a sinusoidal cone.

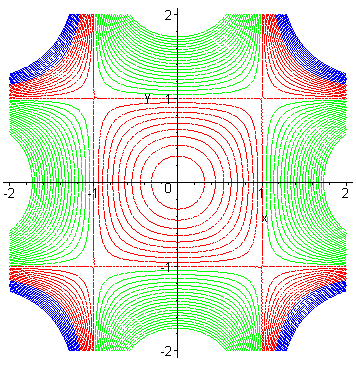
Opposite, the family of quartics with equation , that no longer are rational (in green when k < 0, in red when and in blue when k > 1).
The crosscurve is obtained for k = 1 (limit between the blue and red curves).
When k > 0, they are the contour lines of Bouligand's cushion.

The inverse of the rectangular crosscurve with respect to its centre is the quadrifolium, and its reciprocal pedal, the astroid.

See here the orthoptic of the crosscurve.
Compare with the biaxial inverse of an eight.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra