Reduced Cartesian equation:  (with (0,1,0) as a point at infinity, i.e. a vertical asymptotic direction)

The circularcubics are the cubics passing by cyclic points. It can be proved that they are the cyclic curves for which the initial curve is a parabola. In other words, they are the envelopes of circles the centres of which describe a parabola, and such that a fixed point (the pole) has a constant power with respect to these circles (i.e. these circles have an orthogonal or pseudo-orthogonal intersection with a fixed circle, the directrix circle).
They are rational iff this power is zero.

A circular cubic can be obtained by four definitions of this type in the general case. It loses one if it has a symmetry axis. Independently, it loses two or three of these definitions when it is rational (depending on the kind of singularixty).
The poles are the points of the curve where the tangent is parallel to the asymptote.

Examples:
    - the circular hyperbolic cubic : is the envelope of the circles  where . The initial curve is  and the directrix circle .

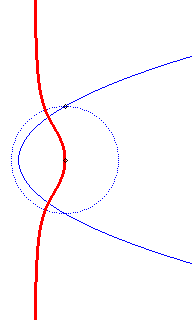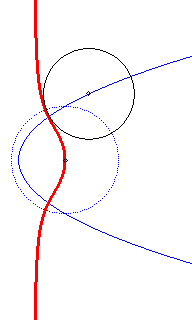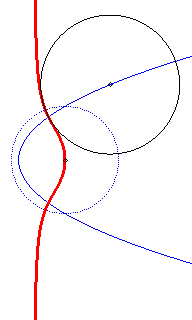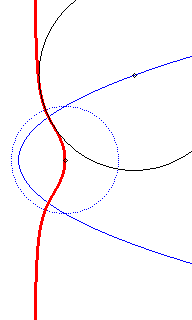Directrix circle in dotted line; the circles, at the beginning, have an imaginary contact with the cubic.

© Robert FERRÉOL 2017