DUPLICATRIX CUBIC

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DUPLICATRIX CUBIC

| Curve studied by Ullhorn in 1809, and G. de Longchamps
in 1890.
Other name: toxoid. |
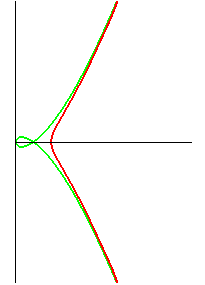
View with the asymptotic cubic 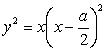 (in green).
(in green). |
Polar equation: Cartesian equation: Cartesian parametrization: Rational cubic (even polynomial) with an isolated point (0,0), that is not obtained with the polar equation. |
Given two perpendicular lines D1 (here Ox) and D2 (here x = a) and a point O on D1, the duplicatrix cubic is the locus of the point M on a variable line D passing through O such that the projection on D of the projection of M on D1 is a point on D2.
This curve is a special case of divergent parabola and of Clairaut's curve.
It is also the inverse of the simple folium with respect to its "pointed" summit,
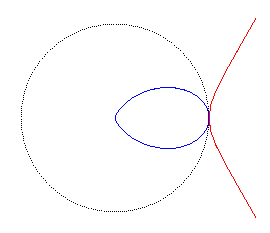
As one can tell by its name, it is a duplicatrix:
indeed, when
,
.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017