Let h be an nondecreasing odd function on 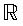 , its values ranging from -1 to 1 (for example , its values ranging from -1 to 1 (for example 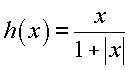 or h = tanh) and let or h = tanh) and let 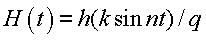 . The plot of H on . The plot of H on 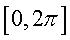 presents with n external notches and n internal notches, more or less deep depending on whether k is more or less large, and more or less high depending on whether q is more or less large. Opposite, n = 5, k = 10, q = 2. presents with n external notches and n internal notches, more or less deep depending on whether k is more or less large, and more or less high depending on whether q is more or less large. Opposite, n = 5, k = 10, q = 2.
This indentation is then curved as follow: |
 |
If the central curve is parametrized on 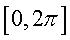 by by 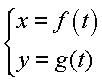 , the notched curve is parametrized by , the notched curve is parametrized by 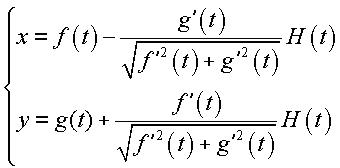
Opposite, the case of a circle; the corresponding curve, with polar equation 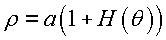 , is called "the notched wheel". , is called "the notched wheel". |
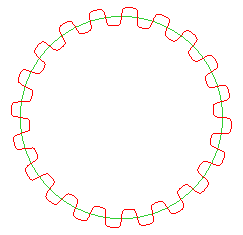
|
| If the parameter t is not proportional to the curvilinear abscissa, the dents do not have the same lengths, as it can be seen in the case of an eight.
Therefore, to get equal dents, the curve has to be parametrized by the curvilinear abscissa. |
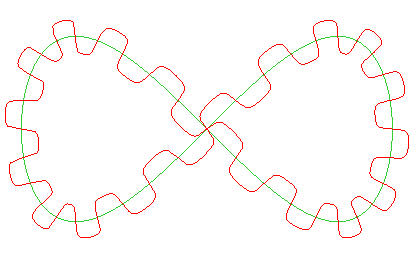
|
| Here is the example of the cycloid, that can easily be parametrized by the curvilinear abscissa. The dents are equal. |
 |

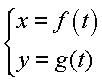 , the notched curve is parametrized by
, the notched curve is parametrized by 

