right serpentine 2
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
FOCAL CIRCULAR CUBIC
| oblique case | right case | |
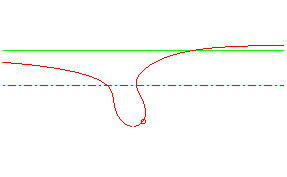
| focal with one branch |
|
|
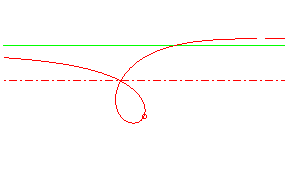
| focal with a knot (strophoid) |
|
|
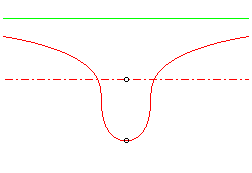
| focal with an oval |
|
|
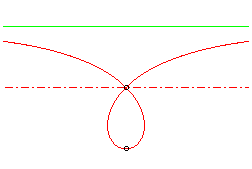
| case where the focus is on the axis |
|
right serpentine 2 |
| Curve studied by Van Rees in 1829, Steiner in 1852 and Laguerre in 1868.
Other: focal of Van Rees, isoptic cubic, Apollonius cubic, circular cubic with an axis (name given in 2002 by Dominique Roux and Michel Tixier). References: [Brocard Lemoyne] III, p. 92 to 100; [Gomes Texeira] I, p. 45 to 58. |
  |
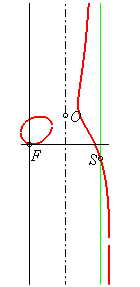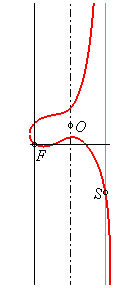The origin is located at the singular focus F:
Cartesian equation:  ,
i.e.  ,
with a ³ 0, b
> 0,
(a = 0: right focal; a = 0: focus on the axis);
the axis is x = a, the asymptote x = 2a, O(a, a tan a) and the intersection point with the asymptote S( 2a, - 2a cot 2a). Circular cubic. Complex equation:  ,
with  .
Polar equation:  ,
with  . |
The focal circular cubics, or just focals, are the circular cubics containing their singular focus F (intersection point between the tangents at the cyclic points); in other words, the cyclic points have the same tangential point (i.e. the point where the tangent cuts the curve again). With the centre of the frame as the origin and the line x = 2a as the asymptote, we get the reduced equation above.
The cubic is elliptic if 
, with an oval if 
, with a branch if 
,
and rational
if 
, in which case we get the strophoids.
The complex equation above shows that the focal circular cubics are the loci of the points M such that the image M' by the composition of an inversion with centre F and a reflection with axis passing by F satisfies the property that the middle of [MM'] describe a line D. This line is called the axis of the focal (hence the name circular cubic with an axis).
The points M and M' are said to be conjugate and can be easily constructed from one another thanks to the fact they have the same tangential point.
 |
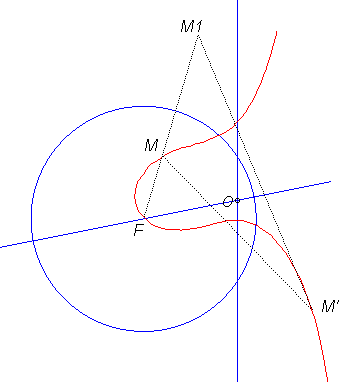M1 is the inverse with pole F of M with respect to the blue circle and M' the symmetrical image of M about (OF).
The middle of [M M'] describes the axis of the focal. The tangents at M and M' intersect at a point on the focal. |
The cubic has a symmetry axis when the axis of the reflection above is perpendicular to that of the focal, in which case it is qualified as right (here, the axis of symmetry is Ox, obtained for 
= 0), or when the focus is on the axis, which is also then the asymptote (here, the axis of symmetry is Oy, obtained for a = 0);
When we are not in the last case, the simplest geometrical construction of the focals is as the contact points between the tangents passing by a point (the focus) to the circles of a pencil of circles. The radical axis of the pencil is the axis of the focal. When the pencil is an intersecting pencil (on the left below), we get the focals with a branch; when it is an nonintersecting pencil, we get the focals with an oval; and when it is singular, we get the strophoids. The centre of the pencil is 
.
The focal is also the locus of the intersection points between the lines passing by F and the circles of the pencil orthogonal to the previous one and centred on these lines.
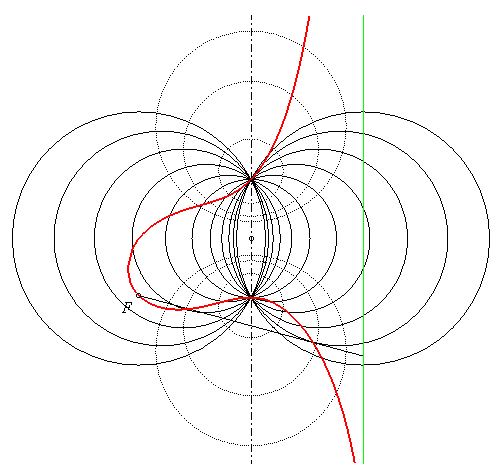
The contact points between the tangents passing by F and the circles of the first pencil describe the focal; the orthogonal pencil is in dotted line. The two base points of the first pencil (limit points of the second one) are the intersection points between the focal and its axis. |
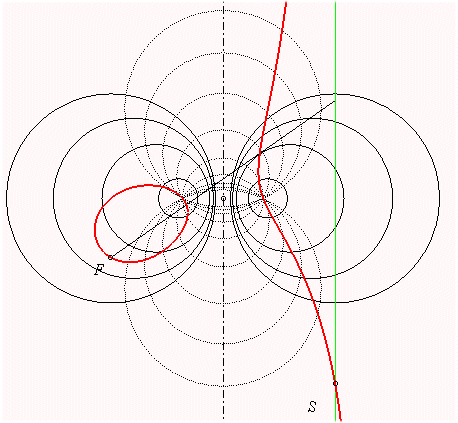The contact points between the tangents passing by F and the circles of the first pencil describe the focal; the orthogonal pencil is in dotted line.
The two limit points of the first pencil (base points of the second one) are the projections of F on the curve. |
Still considering a > 0, the focals also have an elegant 3D construction discovered by Van Rees, as the locus of the foci of conics.
a) In the non-right case ( different from 0).
If S is the intersection point between the focal and its asymptote, O' is the intersection point between the bisector of FSy and the axis, F' is the symmetrical image of F about O' (located on the asymptote) and C is the elliptic cone with vertex S and directrix the ellipse orthogonal to the plane of the focal with semi-axes 
and b, then the focal is the locus of the foci of the conical sections of the cone (C) by planes perpendicular to the plane (OSF) passing by F.
We get a focal with an oval when FF' is the major axis of the directrix ellipse, a focal with a branch when it is the minor axis, and a strophoid when the ellipse is a circle.
 |
 |
S vertex of the cone, M and M'' foci of the conical section of the cone by a plane perpendicular to (OSF) passing by F; the centre I of the conic describes the axis of the focal. |
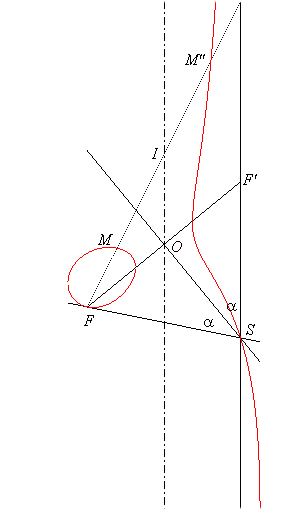
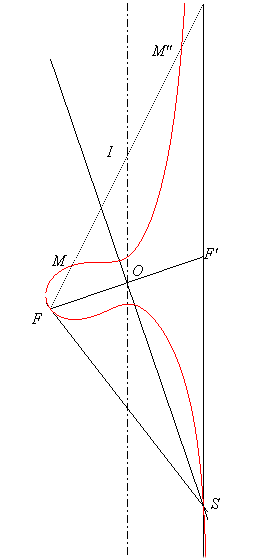
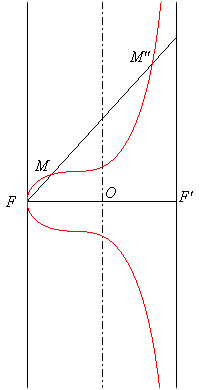
b) In the right case ( = 0).
If (C) is the cylinder with axis the axis of the focal and directrix the ellipse orthogonal to the plane of the focal with semi-axes OF = a and b, then the focal is the locus of the foci of the conical sections of the cylinder (C) by the planes perpendicular to the plane of the focal and passing by F.
We get a focal with an oval when FF' is the major axis of the directrix ellipse, a focal with a branch when it is the minor-axis, and the Newton strophoid when this ellipse is a circle.
 |
 |
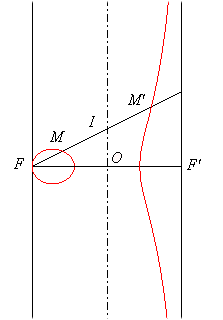M and M'': foci of the conical section of the cylinder by a plane perpendicular to the plane of the focal passing by F; the centre I of the conic describes the axis of the focal. |
Interpretation as an isoptic cubic.
| Given two points A and B on a focal, and the two conjugate points A' and B', the associated focal is the locus of the points M where the oriented segment lines [AB] and [B'A'] are seen under the same angle (i.e. the angles (MA,MB) and (MB',MA') are equal), hence the name isoptic cubic also given to the focals.
Conversely, given two oriented segment lines [AB] and [B'A'] in the plane, the locus of the points where these segment lines are seen under the same angle is in general a focal.
|
 |
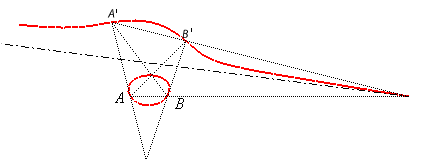
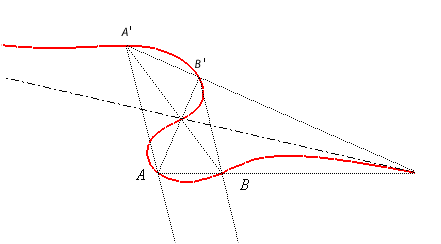| Animation of this construction. |  |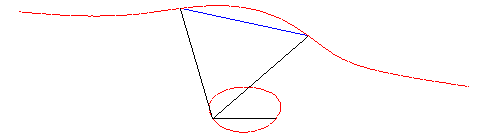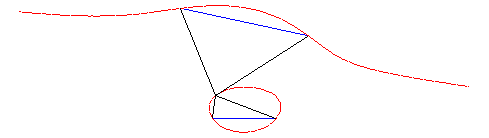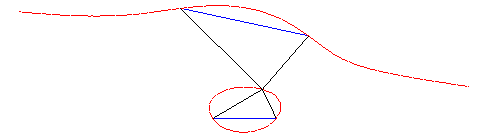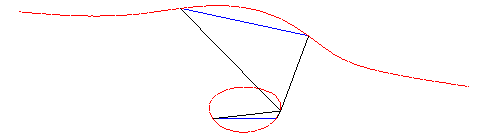
 |
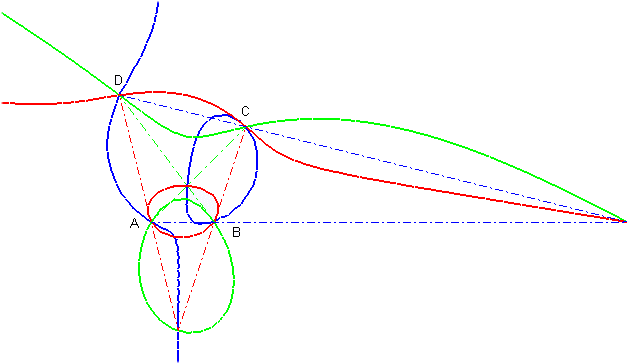4 points A,B,C,D such that the 6 lines joining them are secant, two by two, define three focals:
The red focal is the locus of the points M such that (MA,MB) = (MC, MD), or (MA, MC) = (MB, MD); therefore, it passes by the intersection point between (AB) and (CD) and the intersection point between (AC) and (BD). The blue focal is the locus of the points M such that (MA, MC) = (MD, MB) or (MA, MD) = (MC, MB); therefore, it passes by the intersection point between (AC) and (BD) and the intersection point between (AD) and (BC). The green focal is the locus of the points M such that (MA, MD) = (MB, MC) or (MA, MB) = (MD, MC); therefore, it passes by the intersection points between (AD) and (BC) and the intersection point between (AB) and (CD). |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2017
if they are; this explains the name "Apollonius cubic" also given to the focals, even though Apollonius did not consider them.