Folioid

FOLIOID

Curve studied by P. van Geer in 1918.
Loria 3D p. 240

Polar equation: with n real > 0, i.e. with .
Algebraic curve iff n is rational: if p and q are the numerator and denominator of n, the degree is 2(p +q) if p and q are odd, and 4(p + q) otherwise.
For n =1, it is the circle with centre (b, 0) and radius a.
For a = b (e = 1), it is the rose .

Case e < 1: the curve is rather close to a double conchoid of a rose: ):

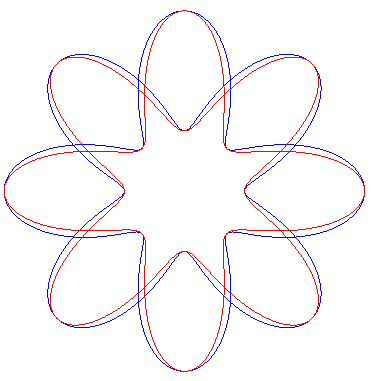In blue, the two conchoids of a rose, and in red the folioid, here with n = 4.

Case e > 1: the curve is composed of p closed curves if p and q are odd, and 2p curves otherwise.

n = 1: circle
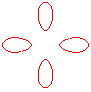
n = 2
n = 3
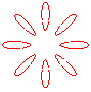
n = 4
n = 5

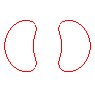
n = 1/2
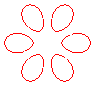
n = 3/2
n = 5/2
n = 7/2
n = 9/2

n = 1/3
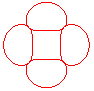
n = 2/3
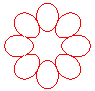
n = 4/3
n = 5/3
n = 7/3

n = 1/4
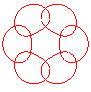
n = 3/4
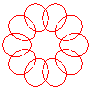
n = 5/4
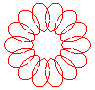
n = 7/4
n = 9/4

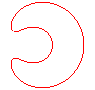
n = 1/5
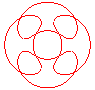
n = 2/5
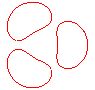
n = 3/5
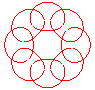
n = 4/5
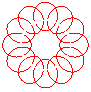
n = 6/5

If it is wrapped around the plane of the circle into a cone with vertex O and half-angle , with axis Oz, the projection on xOy of this wrapped around circle is the folioid . This provides a construction of folioids based on a simple circle in the case n < 1.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

n = 1: circle	n = 2	n = 3	n = 4	n = 5
n = 1/2	n = 3/2	n = 5/2	n = 7/2	n = 9/2
n = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5