Cartesian folium

CARTESIAN FOLIUM

Curve studied by Descartes and Roberval in 1638 then by Huygens in 1672.
From the Latin folium "leaf".
René Descartes (1596-1650): French philosopher, mathematician and physicist.
Other name, given by Roberval: jasmine flower.

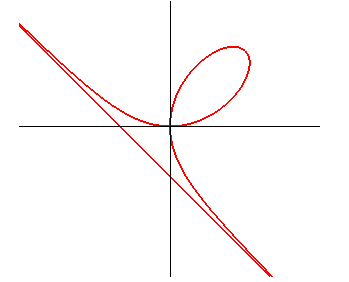Cartesian equation:

.
Polar equation:

.
Cartesian parametrization:

.
Rational cubic with a double point.

The area of the loop is equal to that of the domain located between the curve and its asymptote (of equation x + y = –a); common value: 3a²/2.

The Cartesian folium is, in general, not defined by a geometrical property, but by its Cartesian equation, given above.
The Cartesian equation in a frame turned by p/4 with respect to the previous one is: where b = , equation to relate to that of the Maclaurin trisectrix: . Therefore, the Cartesian folium is none other than the image of this trisectrix by a dilatation of the axis Ox by a ratio .

The Cartesian folium is therefore also a cissoid of an ellipse and a line (images by the above transformation of the circle and the line associated to the Maclaurin trisectrix), so a cissoid of Zahradnik.

See also trident of Newton.

The cubic surface cut by the plane z = 0....

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra