PARABOLIC FOLIUM

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PARABOLIC FOLIUM

| Curve studied by Gérard de Longchamps in 1890. |
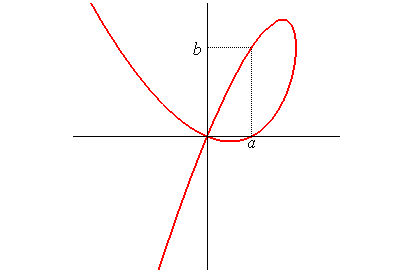 |
Cartesian equation: Polar equation: Rational cubic with a double point. |
Given a point O and two perpendicular lines (D1) and (D2) (here, the lines x = a and y = b), a variable line (D) passing by O meets (D1) at P; the perpendicular at P meets (D2) at Q; the perpendicular at Q meets (D2) at R; the perpendicular at R meets (D) at M: the parabolic folium (which is not a folium) is the locus of M.
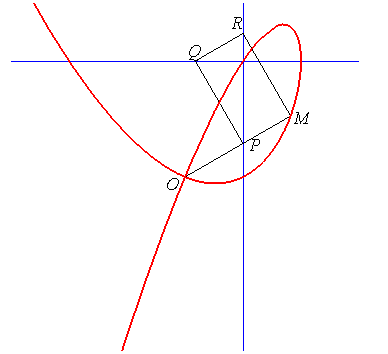
| The parabolic folium is said right when D2
passes by O (b = 0), in which case it is symmetrical about
(D2). Therefore, it is a special
case of divergent
parabola and of tear drop.
Its equation, in the form |
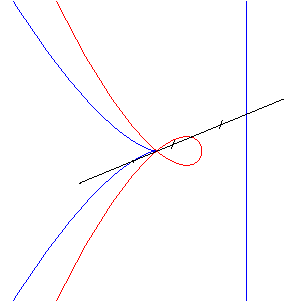 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017