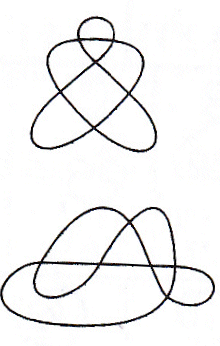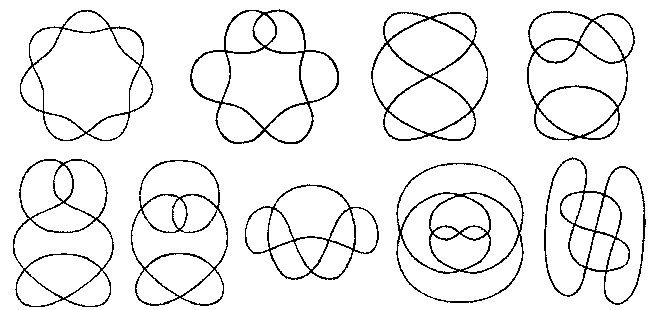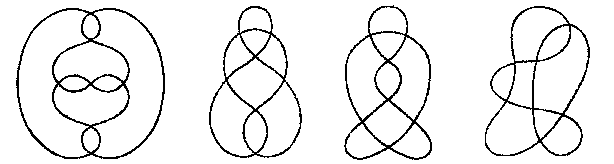GENERIC (CLOSED) CURVE
A generic (closed) curve, plane (or spherical), is (in
Arnold's sense) an equivalence class of closed curves of the plane or the
sphere for which the multiple points are double points with different tangents,
two curves being identified if they are images of one another by a diffeomorphism
of the plane (or the sphere). This notion is a generalisation of that of
Jordan curve to the case where the
curves have crossing points.
By closed curve
we mean, here, the image C of [0,1] by an application f of
[0,1] into the plane (or the sphere), of class C1,
the derivative of which never vanishes, such that f (0) = f (1)
and f ' (0) = f ' (1). The condition for the multiple points
to have different tangents can be written: for all point M of C,
there exist either one or two values t1
and t2 in [0,1[ such that f(t1)
= f(t2) and in this case, 
are not collinear.
The distinction between plane curve or curve traced on
the sphere is important; for example, an eight 
is equivalent to a limaçon with a loop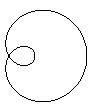 
on the sphere but not in the plane.
Here are various interesting cases providing a classification
of generic curves:
1) the (necessarily finite) number n of double
points; they determine n + 2 regions of the plane, and the curve
is the reunion of 2n arcs joining two consecutive double points.
2) the rotation index (see the
notations): ,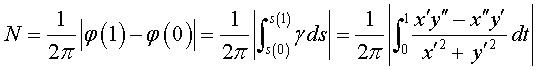
counting the number of times that the tangent completes a whole turn on
itself.
It can be proved that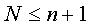 
and that n and N have opposite parity.
These properties are consequences of the following result (Whitney
formula): given a path on the curve, a double point is said to be positive
if, in the second passage by this double point, the first passage had been
made from left to right, and negative otherwise. If n+
is the number of positive double points and n- the number
of negative ones, then N = |n+ - n-|
± 1.
3) the Gauss diagram (see the article above). |
Here there are n = 6 double points, 8 regions, 12 arcs.
Rotation index N = 3 = |2 - 4|+1 |
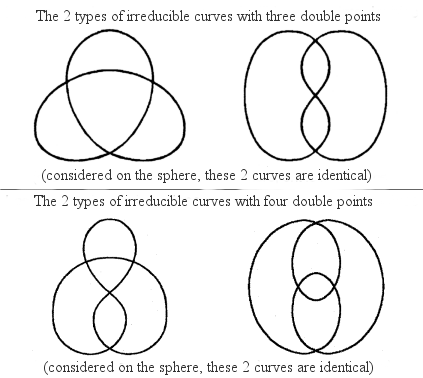
A generic curve is said to be irreducible if it
is still connected after removing one of its double points (for example,
an eight is not irreducible).
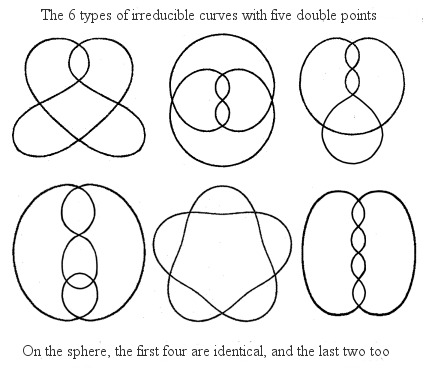
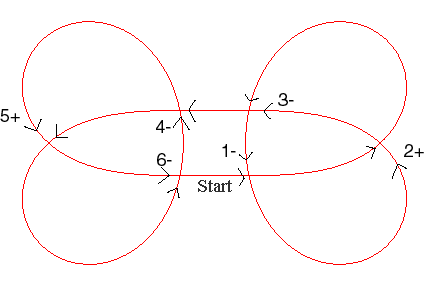
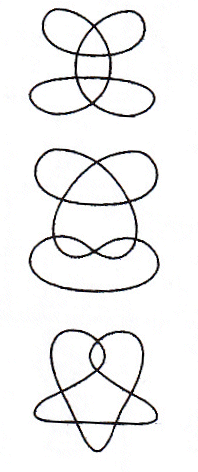
Below, a classification of the plane and spherical irreducible
generic curves having up to 7 double points:
0 double point: 
, none with only 1 or 2 double points,
| n = 6 (Arnold 1994): 5 spherical curves providing
22 plane irreducible curves |
n = 7 (Guy Valette 2004): 13 spherical curves
providing 78 plane irreducible curves |
 
|
|
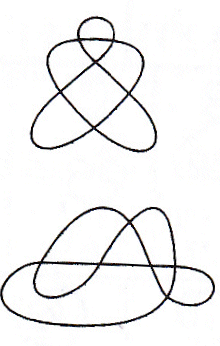
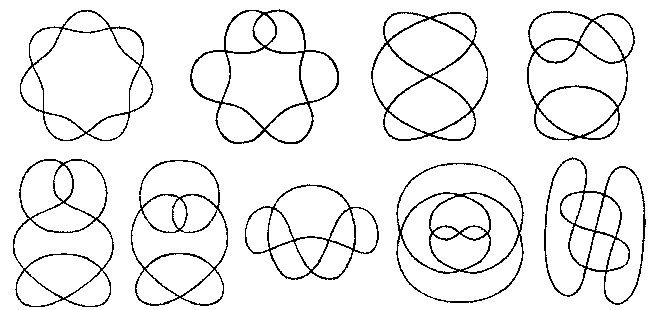
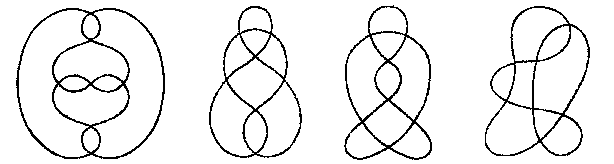
Compare to prime
knots.
See Goursat curve
for the classification of generic curves with n double points having
the symmetries of a regular n-gon.
© Robert FERRÉOL
2017
