CURVE OF CONSTANT GYRATION
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CURVE OF CONSTANT GYRATION

| Curve studied by myself after a question by Franck
Rolland.
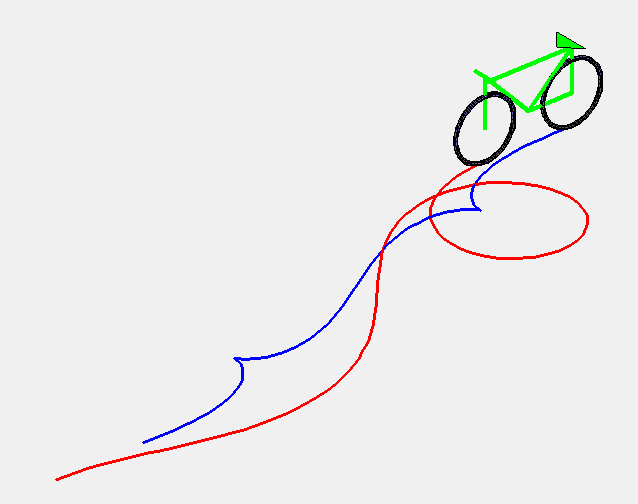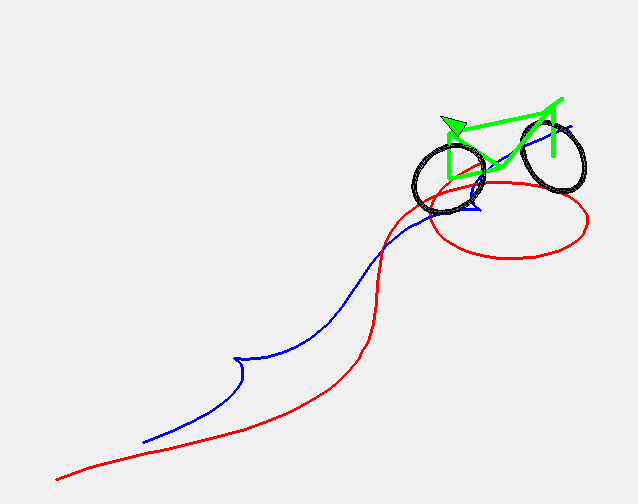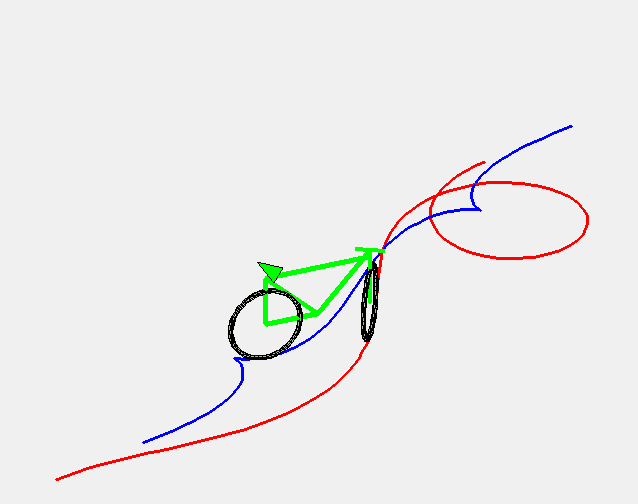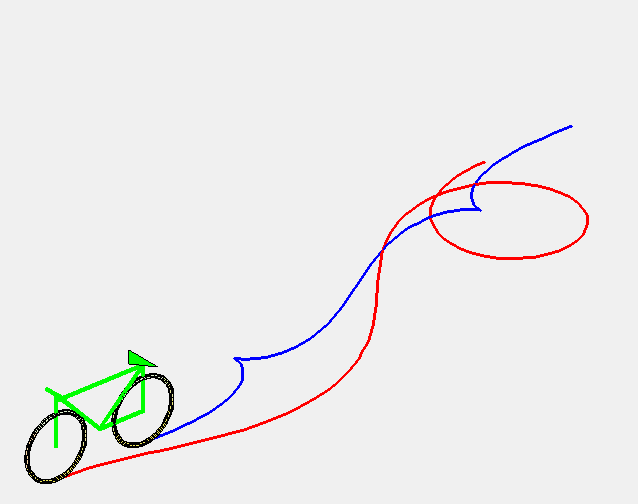
Animation above made by Alain Esculier. |
| 1) Curve of the front wheels:
Cartesian parametrization: Curvilinear abscissa: Intrinsic equation 1: 2) Curve of the back wheels: |
The curve of constant gyration is the curve described by the front wheels of a car (or better, a bike) moving at constant speed while the driver turns the steering wheel at constant speed.
More precisely, it is the curve such that a line (D) passing by a point M of the curve and forming an angle with the tangent proportional to the curvilinear abscissa ((D) is the axis of the car and the point M is the front wheels) remains tangent to a curve at a point N (the back wheels) located at a constant distance from M.
Therefore, it is also the curve the tractory of which is such that the leash forms an angle with the tangent that is proportional to the curvilinear abscissa.
Here are some animations of the movement for a full rotation of the steering wheel, with an increasing speed of rotation.
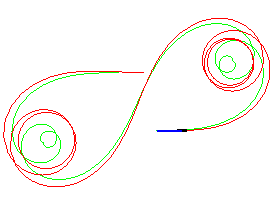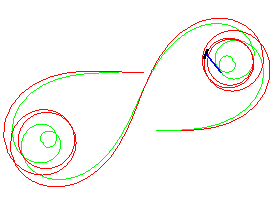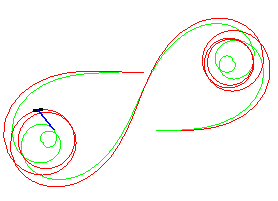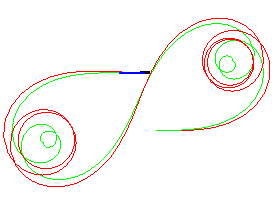
k = 0,1 |

k = 0,2 |

k = 0,3 |

k = 0,4 |

k = 1 |
k = 5 |
Note that if the curve of the front wheels after the steering wheel has completed a whole curve is the perfect copy of the curve before, that of the back wheels is copied only after a half-turn.
| Evolution of the curve on two periods for k increasing from 0.1 to 1 and then, below, to 5 (increasing speed of rotation of the steering wheel).
Notice a form of unrolling of the clothoid until it becomes a sort of elongated cycloid.  |
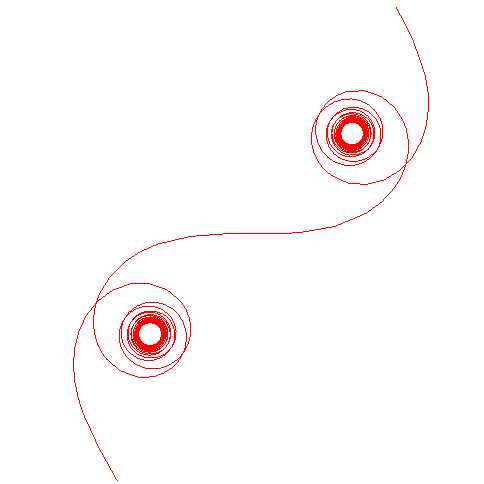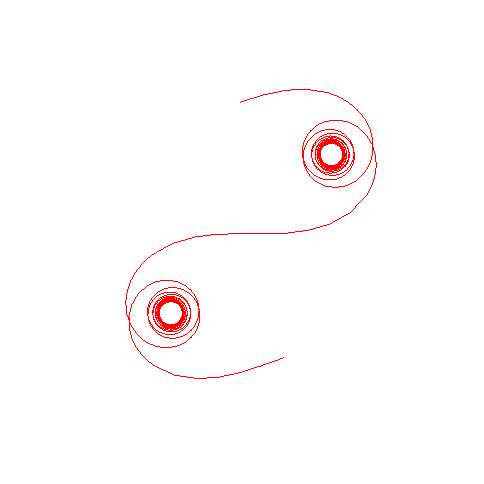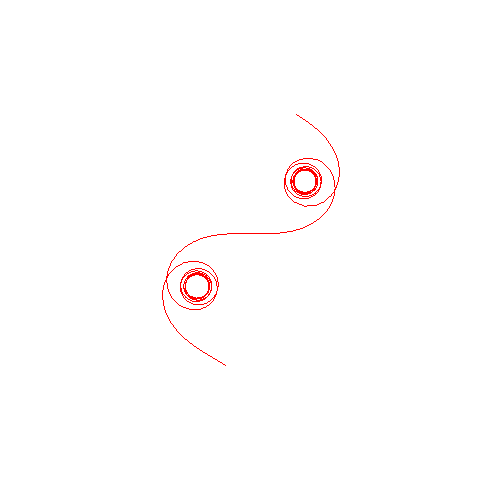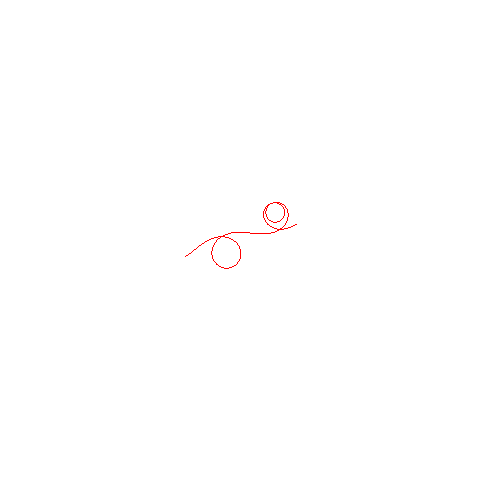 |
| When k goes to 0, the curve of constant gyration coincides with the clothoid:
|
The curve is closed for values k such that 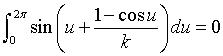 ), such as, for example, k = 0.261 below: ), such as, for example, k = 0.261 below:
 |
Proof of the calculation of the intrinsic equation above:
| Front wheels: Back wheels: Reminder: The collinearity between the speed of the back wheels and so that |
The problem can be generalised to the case of any variation of the steering angle; here is for example an animation of the case of a sinusoidal variation:

Compare to the curve with sinusoidal radius, for which the radius of curvature varies as a sinusoidal function of the curvilinear abscissa (whereas here it is the curvature that is a sinusoid).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017