CURVE WITH SINUSOIDAL RADIUS
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CURVE WITH SINUSOIDAL RADIUS

| Curve studied by L. Bieberbach in 1932. |
The curves studied on this page are the curves the radius of curvature of which is a sinusoidal function of the curvilinear abscissa.
| Intrinsic equation 1: Intrinsic equation 2 when 0 Intrinsic equation 2 when Intrinsic equation 2 when |
 |

curve when lambda = 1 |

curve when n =1 (i.e. lambda = sqrt(2)) |
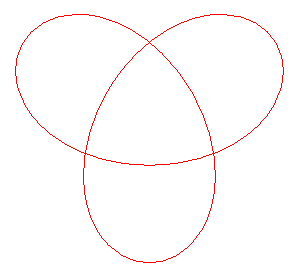
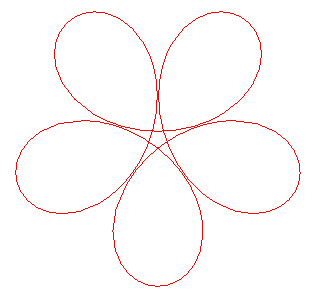
curve when n =3/2 (i.e. lambda = sqrt(13/9)) |

curve when n =2 (i.e. lambda = sqrt(5)) |

curve when n =3 (i.e. lambda = sqrt(10)) |
| If the value of n and lambda are made independent from one another in If n is rational, they are Goursat curves of order the numerator of n.
|
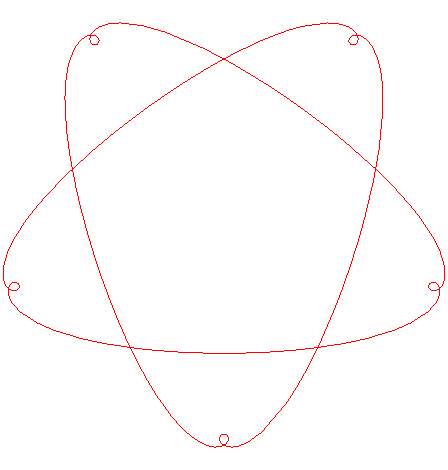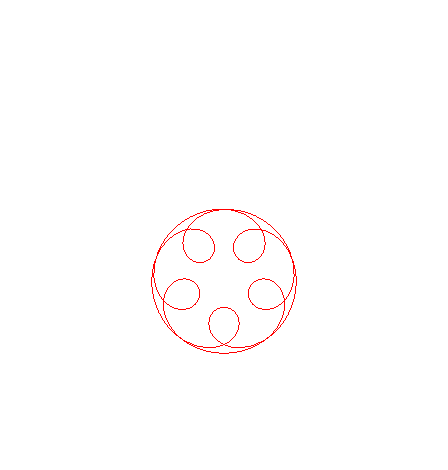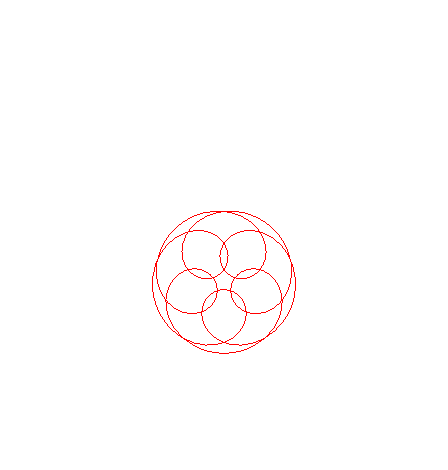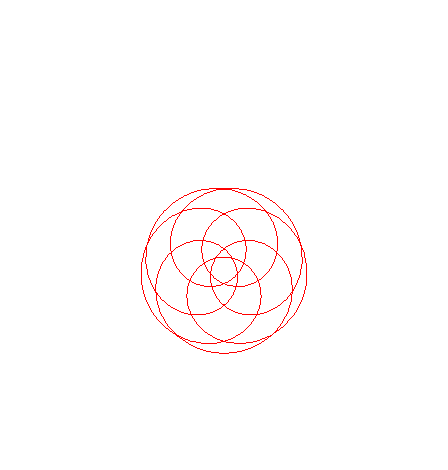 |
| If, now, we consider that the amplitude of the sinusoid varies, we can study the family curves with intrinsic equation 1 Opposite, an animation with k ranging from 0 to 3, with a stop for k =1 which corresponds the case |
 |
The curves the curvature of which varies as a sinusoidal function of the curvilinear abscissa are the meander curves.
Other curves defined by their intrinsic equation: the clothoid, the curve of constant gyration, the syntractrix curve.
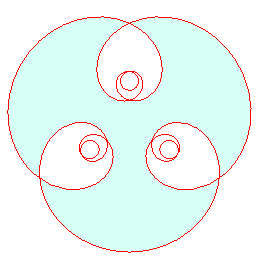
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017