Glissette

GLISSETTE

Notion studied by Catalan in 1865 and by Besant in 1869.
See [Brocard].

The glissettes are curved traced on a fixed plane by a point on a moving plane, the motion of the moving plane being described by the movement of two of its curves sliding on two curves of the fixed plane.

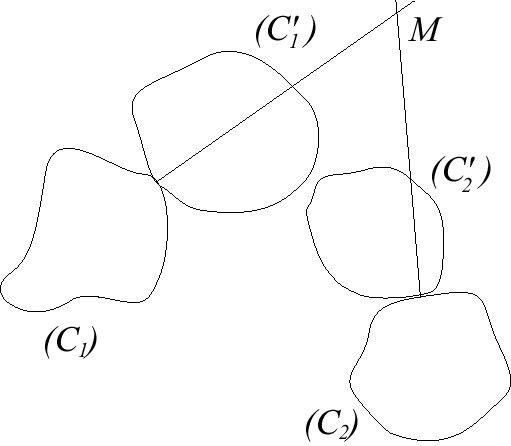
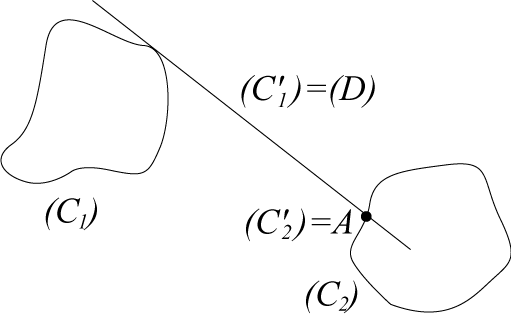
More precisely, let (C₁) and (C₂) be two curves of a fixed plane (the bases), and (C'₁) and (C'₂) two curves of the moving plane (the sliding curves): the motion of the moving plane is determined by the fact that (C'₁) stays tangent to (C₁) and (C'₂) to (C₂). The associated glissettes are the traces of a point of the moving plane on the fixed plane.

Note that since all motions of a plane over a fixed plane are described by a rolling curve rolling on a base, any glissette is in fact also a roulette.
The base and the rolling curve of the motion of a plane over a fixed plane can be obtained as follows: the common normal to (C₁) and (C'₁) at the sliding point and the normal to (C₂) and (C'₂) intersect at M which is the instant centre of rotation of the moving plane with respect to the fixed plane. The base is the locus of M in the fixed plane, and the rolling curve is that of M is the moving plane.

From this we derive a beautiful duality theorem: if the bases and sliding curves are swapped (i.e., (C'₁) and (C'₂) are fixed and (C₁) and (C₂), respectively, slide over them), then the base and the rolling curve of the motion of a plane over a fixed plane are also swapped.
(see applications of this theorem on this page).

SPECIAL CASE N° 1 (original case, that gave rise to the notion of glissette)

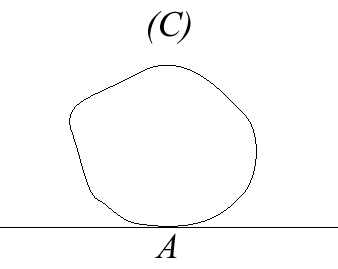
Case where (C₁) is a line (D), (C₂) is reduced to a point A on the line (D), and (C'₁) and (C'₂) coincide (and we write them (C)); the motion of the moving plane is therefore defined by the fact that the sliding curve (C) stays tangent to the line (D) at the point A.
The instant centre of rotation of this movement of a plane over a fixed plane is the centre of curvature at A; the rolling curve is the evolute of (C) that rolls without slipping on the base, which is the normal at A.
We derive from this that the glissettes with linear base of a curve are the roulettes with linear base of the evolute of this curve.
In this case, we get the following formulas:

If the Cartesian parametrization of the sliding curve in the moving plane is , then the base of the sliding motion is the axis Ox and the point A is the centre O,
the glissette of the centre of the frame is parametrized by ;
the sliding curve at the instant t is then parametrized by (parameter u).
If the polar equation of the sliding curve is ,
then the polar parametrization of the glissette of the pole is
Conversely, if the polar equation of the glissette is ,
then the polar parametrization of the sliding curve is .

Examples (see also the roulettes with linear base, according to the theorem above).

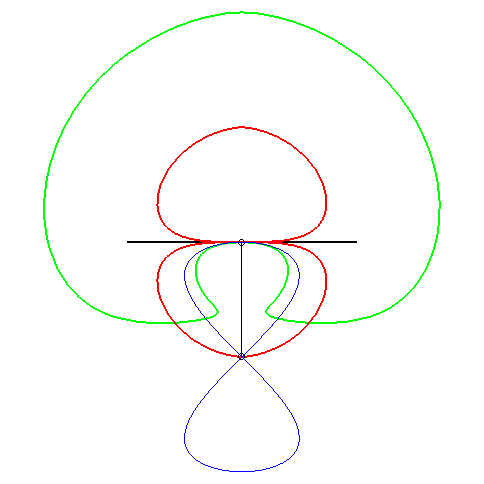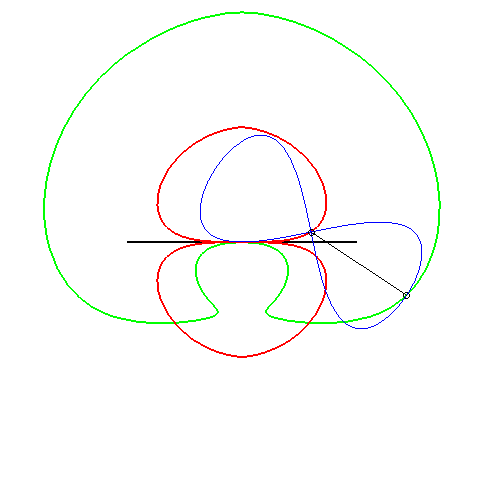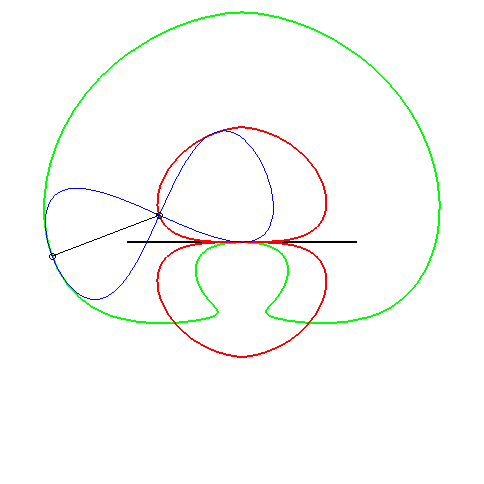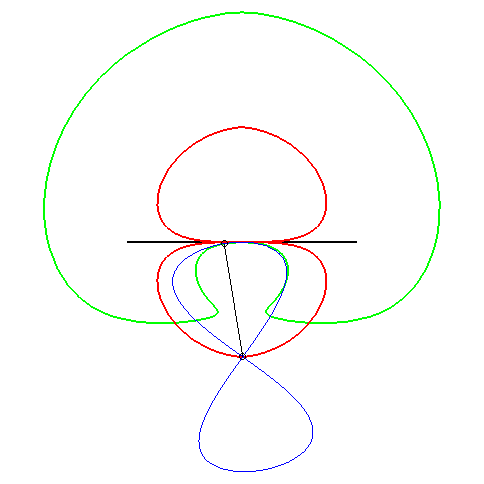
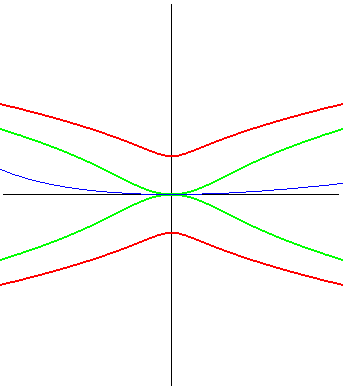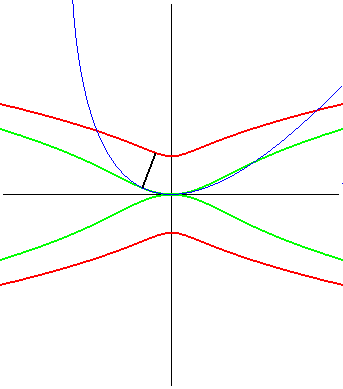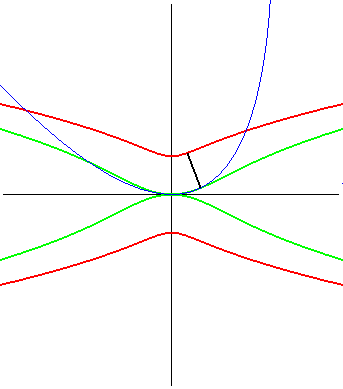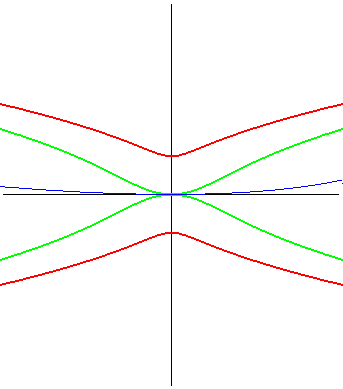
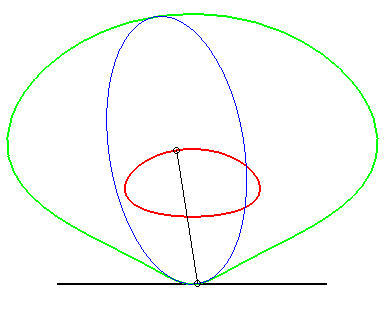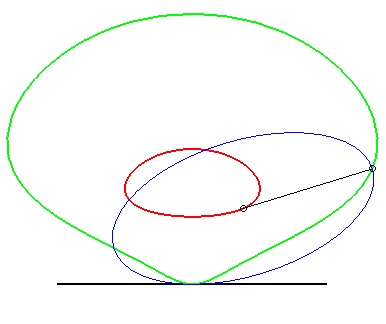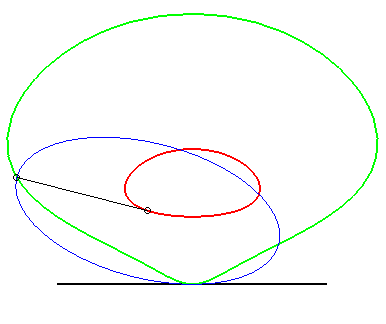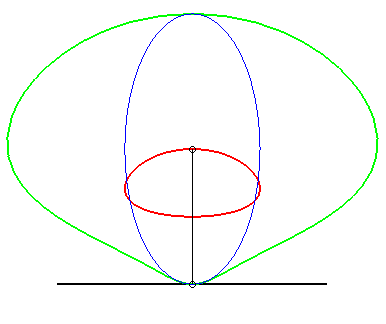
(1) The glissette of the focus of a parabola is a Kampyle of Eudoxus; (2) that of the vertex (in green opposite) is the curve parametrized by
(),
whose equation is: .

(3) The glissette of the centre of an ellipse is a quartic of Bernoulli parametrized by and its equation is ; in green, the glissette of a vertex of the ellipse.
(4) The glissette of the centre of a rectangular hyperbola is the Clairaut's curve r² sin q = a².

(5) The glissette of the tip of a cardioid is a double egg. 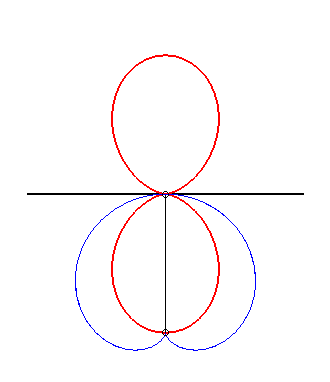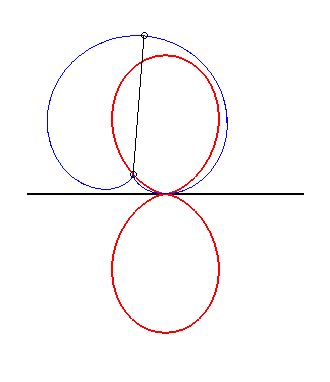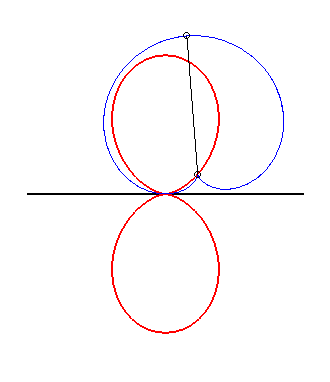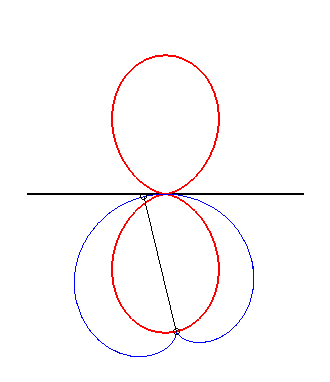(6) The glissette of the centre of a lemniscate of Bernoulli is curve of the dipole.
The previous cases (1),(4),(5),(6) are examples of the fact that the glissettes of sinusoidal spirals are Clairaut's curves: .

(7) The glissette of the pole of an involute of a circle is a straight line (this is normal since the roulette of the centre of a circle (evolute of the involute) rolling on a line is a line!) 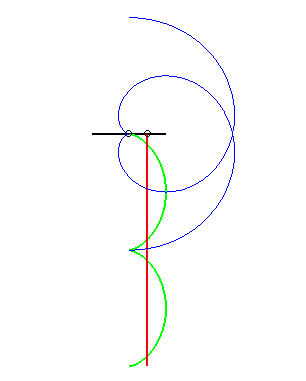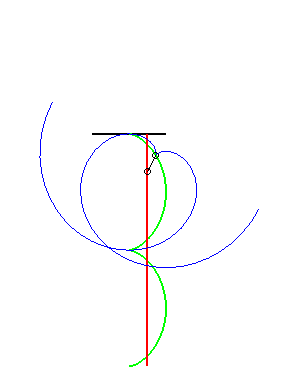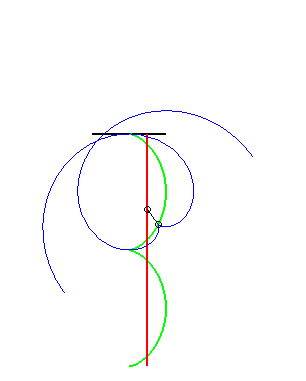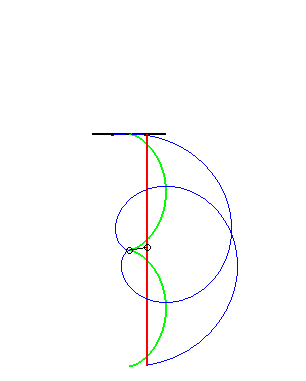(8) The same is true for the glissette of the pole of a logarithmic spiral (it is a consequence of the fact that the angle between the tangent and the radius vector is constant)
The other glissettes are trochoids.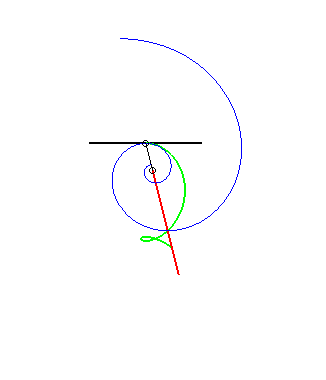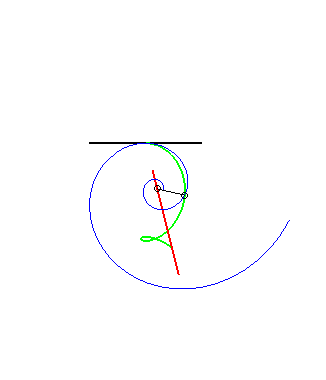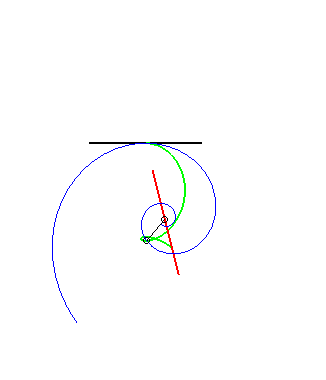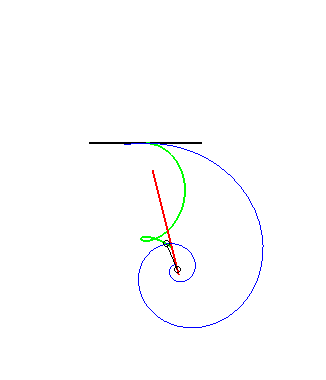

(9) The glissette of the pole of an Archimedean spiral is a Kappa. 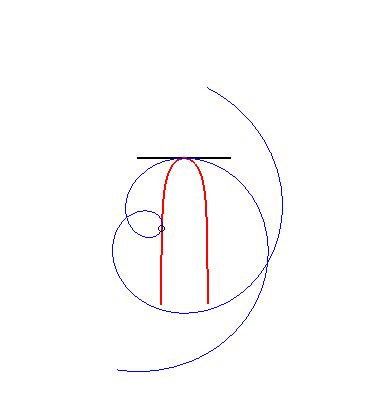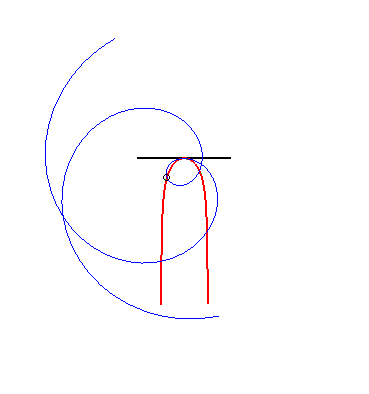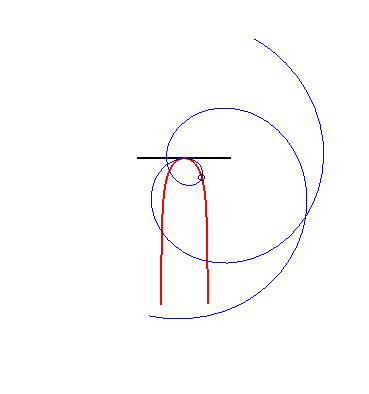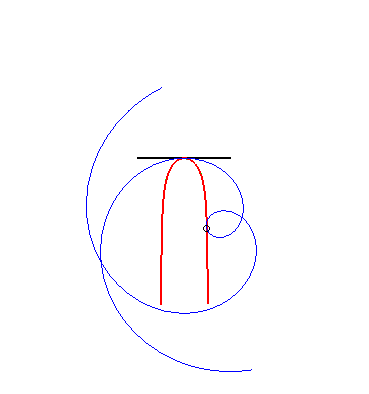(10) The same is true for the glissette of the pole of a hyperbolic spiral.

Last examples: the glissettes of the centre of the fixed circle of a centred cycloid are ellipses (since it is also the case for their roulettes).
The glissette of the pole of a tractrix spiral is a circle.

CASE DUAL TO CASE N° 1

Case where a line slides on a fixed curve (C), the tangency point A being fixed on the line.
The glissette generated by a point on the sliding line is then none other than an equitangential curve associated to the curve (C).
And the glissette generated by a point that is perpendicularly projected on the line on A is none other than a curve parallel to the curve (C).
The base of the associated motion of a plane over a fixed plane is the evolute of (C) and the rolling curve is the normal at A.

SPECIAL CASE N°2

Case where (C₁) and (C₂) are reduced to points A and B, and (C'₁) and (C'₂) coincide like before and are written (C). Opposite, the example of the glissette of the vertex of a parabola passing by two fixed points.
When B tends linearly to A, the case "tends" to the case n° 1.
The dual case is that where the moving plane is carried by two of its points describing a fixed curve (C).
See on this page the different examples where (C) is a conic .

SPECIAL CASE N°3
Other examples where the curves (C'₁) and (C'₂) are still one and the same curve (C):

1) The two curves (C₁) and (C₂) are perpendicular lines:

If an ellipse is constrained to remain tangent to two fixed perpendicular lines, the glissette of the centre of the ellipse is an arc of a circle (inverse property of the fact that the orthoptic curve of the ellipse is a circle).
Opposite we added the glissettes of the vertices of the ellipse.
The general glissette is parametrized by: .
For the complete study, see this PhD thesis p. 30.
Cf also this animation, showing a very simple articulated system yielding the movement of the ellipse.

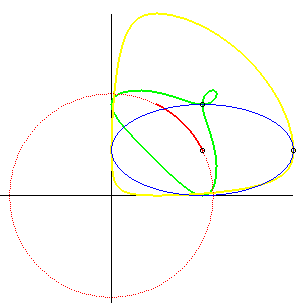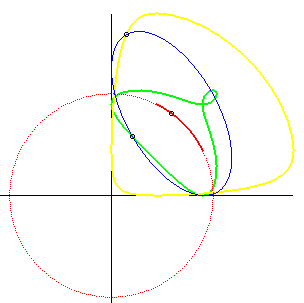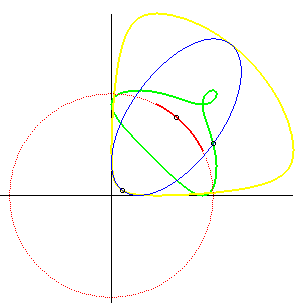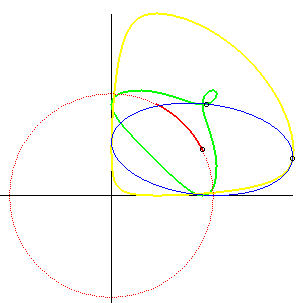The same is true for the parabola: the glissette of the focus of the parabola is then a crosscurve; that of the vertex (in green opposite) is the curve parametrized by: (), whose equation is .
For the base and the rolling curve, see Besant p. 50.

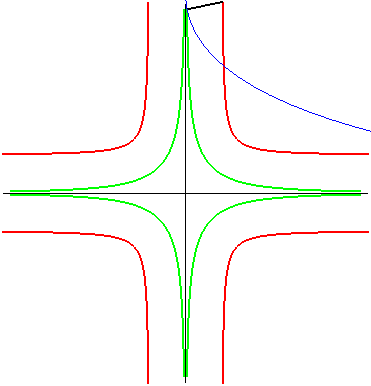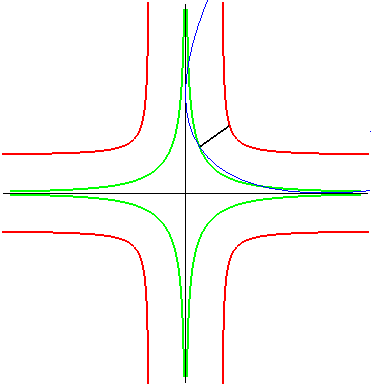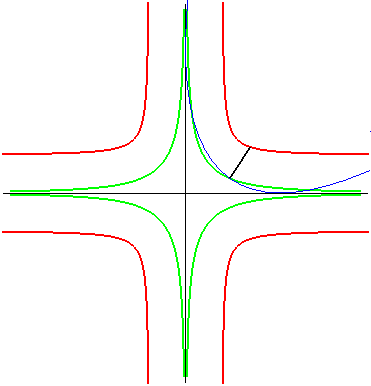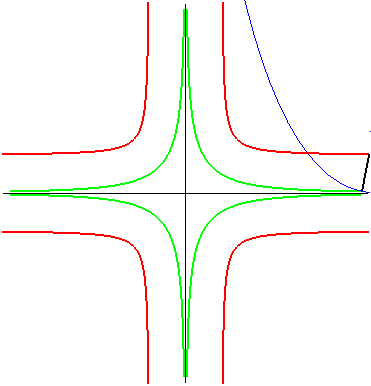In the dual case, the glissette of the intersection point between 2 perpendicular lines tangent to a curve is none other than the orthoptic curve.

2) The curve (C₁) is a line and (C₂) a point not located on this line.
Example of the glissette of the vertex of a parabola:

SPECIAL CASE N°4
The curves (C'₁) and (C'₂) are reduced to points like in the case n°2), but (C₁) and (C₂) are different: the moving plane can be visualised well by the movement of a plank with two removable casters on two rails.

Examples:

Case where the curves (C₁) and (C₂) are perpendicular lines: the glissettes are ellipses; we find here the construction of the ellipse by the method called "of the strip of paper".
Furthermore, the base of the movement of a plane over a fixed plane is a circle, and the rolling curve is a circle with half radius; the points on this rolling curve describe segments of lines: we find here the La Hire device.

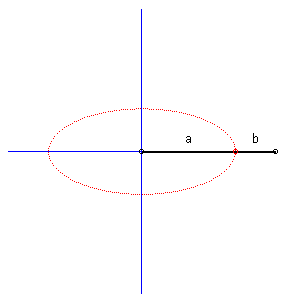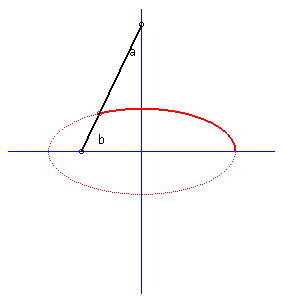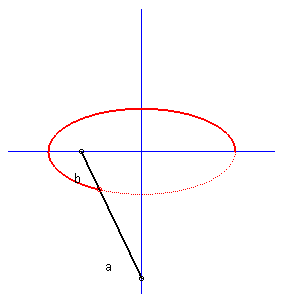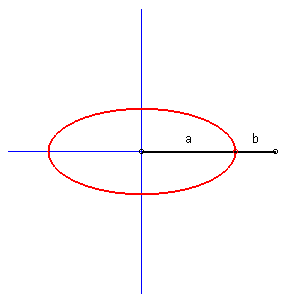If two points on the moving plane slide on two circles, then the glissettes are the curve of the three-bar. When one of the curve is a line and the other one a circle, we get the curves of the slider-crank mechanism and, more generally, when one of them is a line and the other one is a conic, we get the polyzomal curves.

DUAL CASE OF THE CASE N°4
(C₁) and (C₂) are reduced to fixed points M₁ and M₂ , and the two curves (C'₁) and (C'₂) are required to pass through M₁ and M₂.

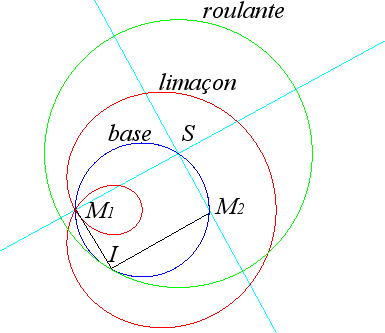
Case where (C'₁) and (C'₂) are two perpendicular lines. Their point of intersection S describes the circle of diameter [M₁M₂].
The points on the line (M₁S) remain at constant distance from S, therefore describe a "conchoid" of the circle described by S, of pole M₁, which belongs to this circle. It is a Pascal's snail.
We let the reader understand from the figure the construction of the base and the rolling curve which are, as expected by duality, a circle and a circle of double radius, the first circle being precisely that described by S. This allows to see that all the glissettes are Pascal's snails.

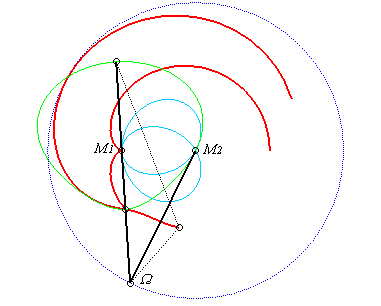
Cas où (C'₁) est (C'₂) sont respectivement une droite et un cercle centré sur cette droite.
Il faut placer une barre double fixée en M₂ et articulée en , la deuxième branche passant par M₁ .
Les glissettes de points qui sont sur la deuxième branche tracent des « conchoïdes » du cercle lieu des points . Voir cette page pour des animations.
Case where (C'₁) and (C'₂) are respectively a line and a circle centered on this line.
It is necessary to place a double bar fixed in M₂ and articulated in , the second branch passing through M₁.The point of the second branch draw "conchoids" from the circle locus of the points . See this page for animations.

SPECIAL CASE N°5

(C'₁) and (C₂) are reduced to points; i.e., a curve (C_m) of the moving plane passes by a fixed point A_f, and a point A_m of the moving plane describes a fixed curve (C_f). Note that the dual case is then of the same type.

If the moving curve is a line and the moving point is located on this line, the glissettes of the points on the moving line are none other than the conchoids of the fixed curve with respect to the fixed point. The others are isoconchoids of it.
Opposite, the case where the fixed curve is also a line. We recognize indeed, in red, a conchoid of Nicomedes; in green, two isoconchoids.
The associated movement of a plane over a fixed plane, called conchoidal movement, is studied on this page.

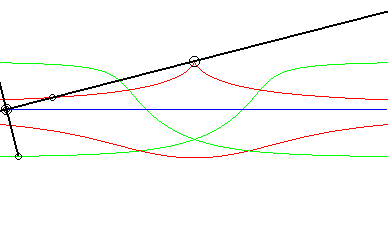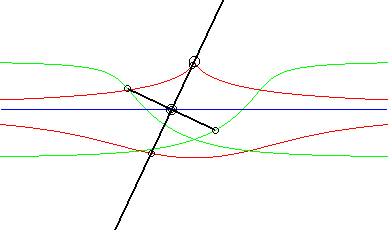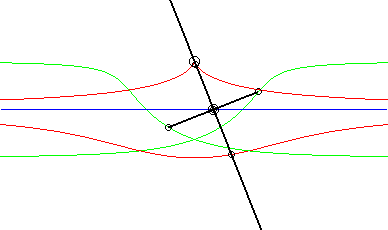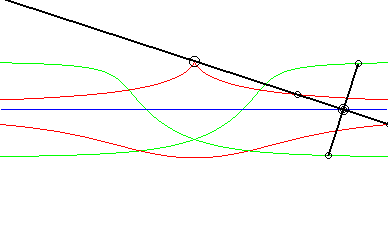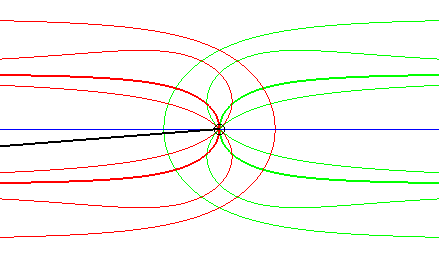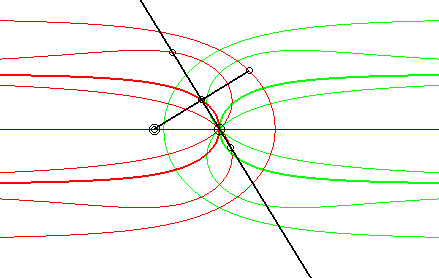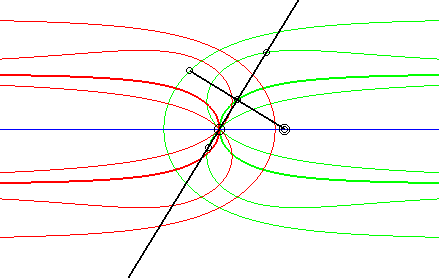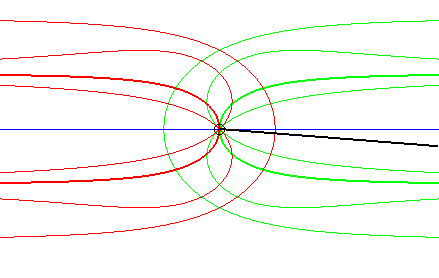
In the dual case, the fixed curve is a line and the fixed point is on this line; the moving curve passes by this point and the moving point describes the line.
Opposite, the case where the fixed curve is also a line. The glissette of the projection of the moving point on the moving line is a Kappa (in bold), hence the name of the associated movement of a plane over a fixed plane: the Kappa movement (see this page).
The other glissettes are conchoids, or isoconchoids, of the Kappa with respect to its centre.

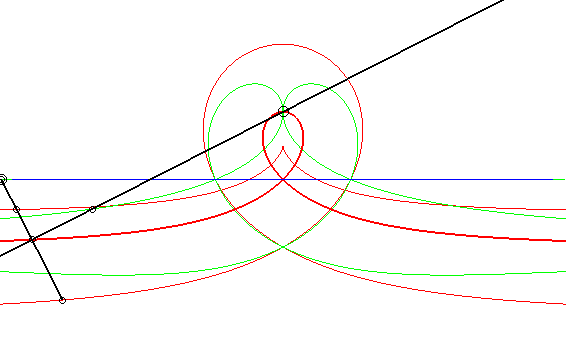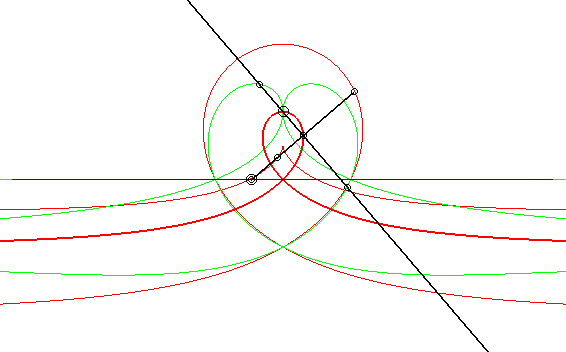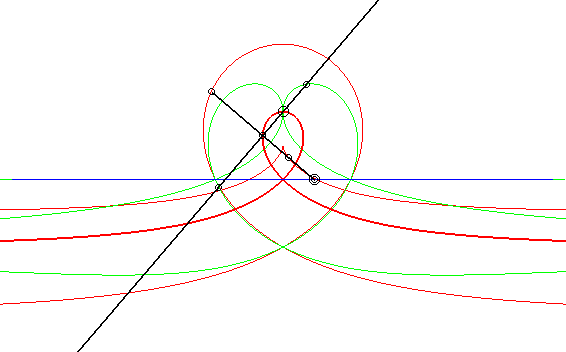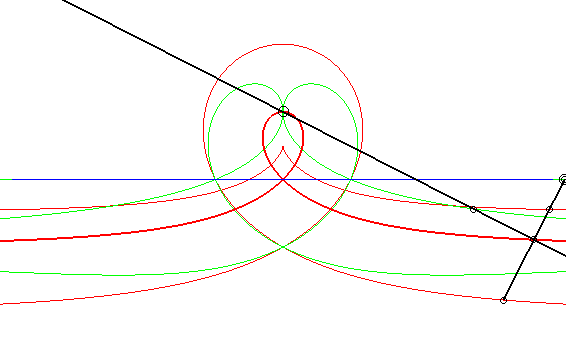
Case where the fixed and moving curves are lines, the fixed and moving points being at the same distance to their associated line.
The glissettes of the points on the line passing by the moving point and perpendicular to the moving line are the right rational circular cubics. We recognize here the mechanism called "Newton's set square" used to trace cubics.
In particular, the glissette of the projection of the moving point on the moving line is a right strophoid (in bold opposite).
The other two red curves are the right cissoid and the Maclaurin trisectrix.
The glissettes of the points on the moving line are the conchoids of the right strophoid with respect to its vertex, i.e. any strophoid (two examples in green opposite).
The other glissettes are isoconchoids of the right strophoid with respect to its vertex.

SPECIAL CASE N°6

(C'₁) is a line (D), and (C'₂) is a point A of this line.
In other words, a point A of a connecting rod (D) is forced to move on a curve (C₂) while remaining tangent to a curve (C₁).

Example: (C₁) is a circle of radius a and (D) is a tangent to this circle.
We look at the glissette of a point of the connecting rod located at a distance b from A.
Parametrization : .
Cartesian equation :.
The basis of the plane-on-plane movement is the parabola with focus the center of the circle and directrix the fixed tangent and the rolling one is the parabola with focus A and directrix parallel to the mobile tangent passing through the center of the circle.
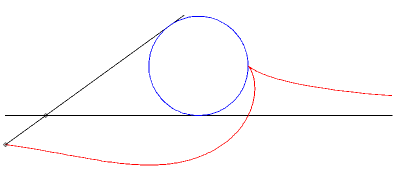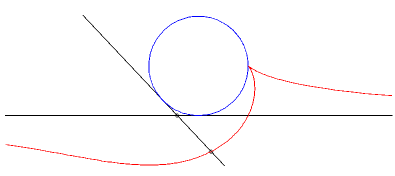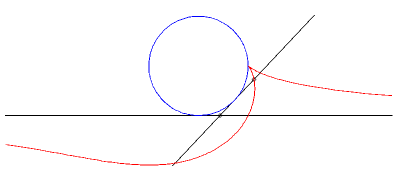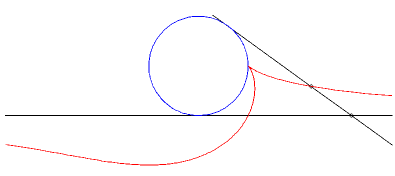
Case a = b : rationnal cuspidal cubique.

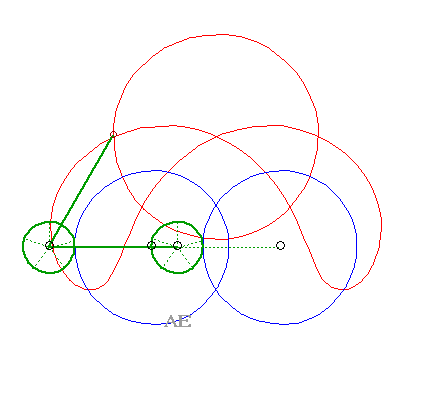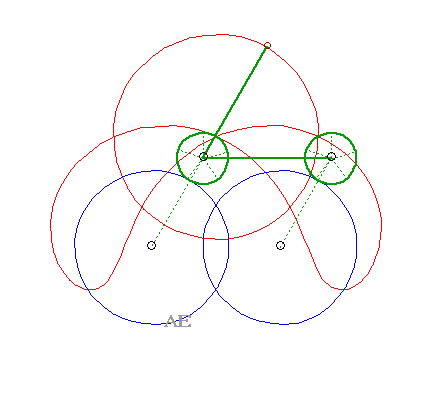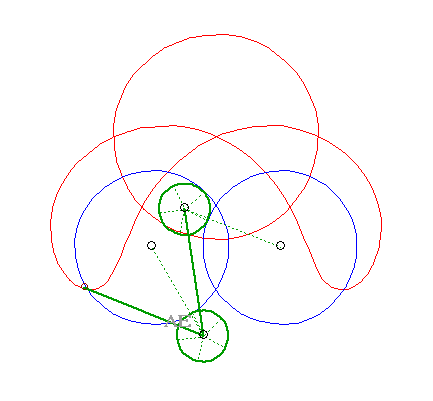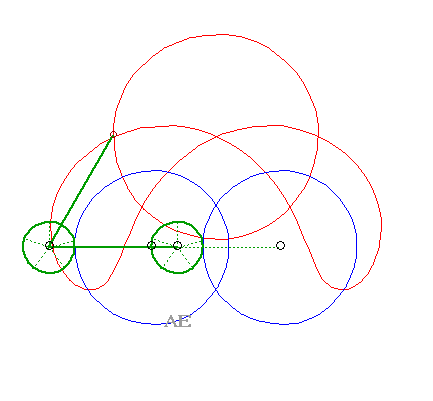
SPECIAL CASE N°6

The 4 curves (C₁) and (C₂), (C'₁) and (C'₂) are circles.
The glissettes are none other, again, than the curves of the three-bar.

This can be generalized by adding a constraint, but allowing the moving plane to be only similar to the fixed plane, and no longer isometric to it.
Examples:

If the focus of a parabola is fixed, and the parabola is constrained to pass by a fixed point, then the glissette of the vertex of this parabola is a cardioid:

Conversely, if the vertex of a parabola is fixed, and the parabola constrained to pass by a fixed point, then the glissette of the focus of this parabola is a cissoid of Diocles:

1) The two curves (C₁) and (C₂) are perpendicular lines:
If an ellipse is constrained to remain tangent to two fixed perpendicular lines, the glissette of the centre of the ellipse is an arc of a circle (inverse property of the fact that the orthoptic curve of the ellipse is a circle). Opposite we added the glissettes of the vertices of the ellipse. The general glissette is parametrized by: . For the complete study, see this PhD thesis p. 30. Cf also this animation, showing a very simple articulated system yielding the movement of the ellipse.
The same is true for the parabola: the glissette of the focus of the parabola is then a crosscurve; that of the vertex (in green opposite) is the curve parametrized by: (), whose equation is . For the base and the rolling curve, see Besant p. 50.
In the dual case, the glissette of the intersection point between 2 perpendicular lines tangent to a curve is none other than the orthoptic curve.

Case where the curves (C₁) and (C₂) are perpendicular lines: the glissettes are ellipses; we find here the construction of the ellipse by the method called "of the strip of paper". Furthermore, the base of the movement of a plane over a fixed plane is a circle, and the rolling curve is a circle with half radius; the points on this rolling curve describe segments of lines: we find here the La Hire device.
If two points on the moving plane slide on two circles, then the glissettes are the curve of the three-bar.		When one of the curve is a line and the other one a circle, we get the curves of the slider-crank mechanism and, more generally, when one of them is a line and the other one is a conic, we get the polyzomal curves.

(C'₁) and (C₂) are reduced to points; i.e., a curve (C_m) of the moving plane passes by a fixed point A_f, and a point A_m of the moving plane describes a fixed curve (C_f). Note that the dual case is then of the same type.
If the moving curve is a line and the moving point is located on this line, the glissettes of the points on the moving line are none other than the conchoids of the fixed curve with respect to the fixed point. The others are isoconchoids of it. Opposite, the case where the fixed curve is also a line. We recognize indeed, in red, a conchoid of Nicomedes; in green, two isoconchoids. The associated movement of a plane over a fixed plane, called conchoidal movement, is studied on this page.
In the dual case, the fixed curve is a line and the fixed point is on this line; the moving curve passes by this point and the moving point describes the line. Opposite, the case where the fixed curve is also a line. The glissette of the projection of the moving point on the moving line is a Kappa (in bold), hence the name of the associated movement of a plane over a fixed plane: the Kappa movement (see this page). The other glissettes are conchoids, or isoconchoids, of the Kappa with respect to its centre.
Case where the fixed and moving curves are lines, the fixed and moving points being at the same distance to their associated line. The glissettes of the points on the line passing by the moving point and perpendicular to the moving line are the right rational circular cubics. We recognize here the mechanism called "Newton's set square" used to trace cubics. In particular, the glissette of the projection of the moving point on the moving line is a right strophoid (in bold opposite). The other two red curves are the right cissoid and the Maclaurin trisectrix. The glissettes of the points on the moving line are the conchoids of the right strophoid with respect to its vertex, i.e. any strophoid (two examples in green opposite). The other glissettes are isoconchoids of the right strophoid with respect to its vertex.