Humbert cubic

HUMBERT CUBIC

Curve studied by G. Humbert in 1887 (j. de math pures et appliquées, 1887, p. 377).
Marie Georges Humbert (1859-1921): French mathematician.
Homemade name.

Polar equation:

.
Cartesian equation:

, i.e.

.
Elliptic cubic.
Curvilinear abscissa given by

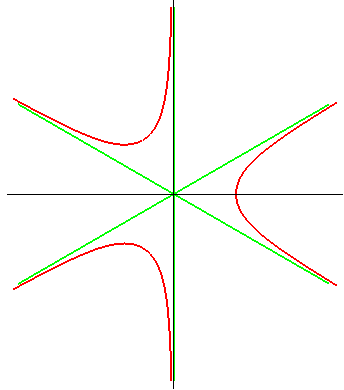The Humbert cubic is the curve defined by the equations above.
Its polar equation shows that it is a special case of sinusoidal spiral (parameter n = –3).
Its Cartesian equation shows that it is a special case of cubic hyperbola.

It is also the inverse of the Kiepert curve.

It was considered by Humbert because it is one of the few cubics, with the Tschirnhausen cubic, for which has a rational expression as a function of x and y (but not as a function of x alone!).

The Humbert cubic and the equilateral trefoil (with similar shape, but the asymptotes of which do not intersect) are the only cubics with a rotation symmetry of order 3 (see Goursat curve).

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra