Hence the kinematics equations of motion:
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
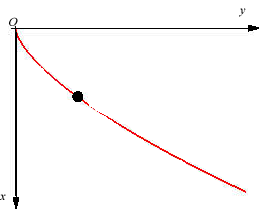
ISOCHRONOUS CURVE OF LEIBNIZ
| Curve studied by Leibniz in 1687 and by Jacques Bernoulli in 1690.
Wilhelm Gottfried Leibniz (1646 - 1716): German philosopher and scholar. |
 |
With Ox as the descending vertical axis and a starting point at O with zero horizontal speed, the conservation of energy gives Hence the kinematics equations of motion: |
An isochronous curve of Leibniz is a curve such that if a particle comes down along it by the pull of gravity, the vertical component of the speed is constant, when the gravitational field is supposed to be uniform.
The solution is a semicubical parabola, as shown in the above derivation. Note that the initial speed at the vertex of the parabola must be equal to for the semicubical parabola
to be isochronous; the vertical component is then a constant equal to
(and the horizontal component is proportional to the square root of time).
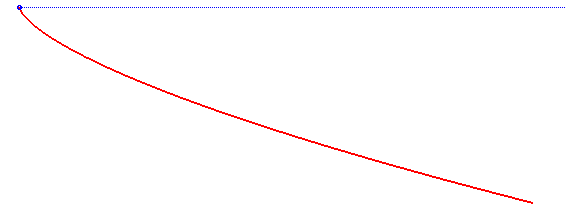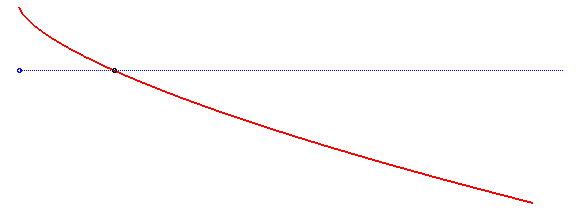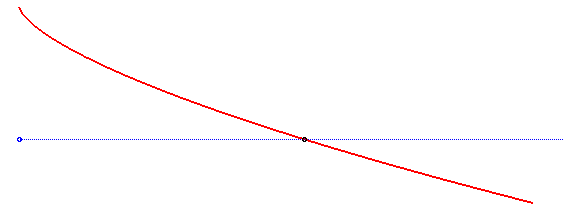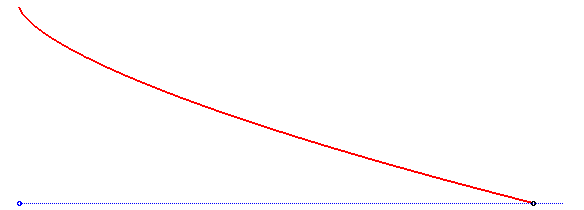
In this derivation, the acceleration vector of the gravity force was supposed to be constant; if it is only supposed to have constant norm, but is oriented in the direction of a point at finite distance, then we get the curves called isochronous curves of Varignon.
For other curves of motions of a massive point in a gravitational field subject to certain conditions, see the
isochronous curves of Huygens, the paracentric isochronous curve, the tautochronous curves, the synchronous curves and the curve of constant reaction.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017