Complex parametrization: , where , is the circle passing by A(a,0) if . Quartic?

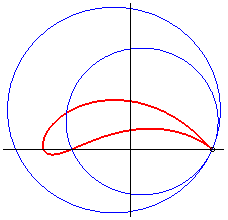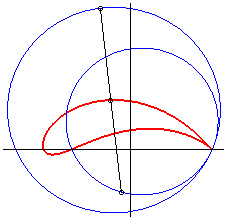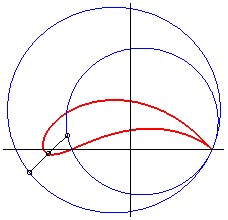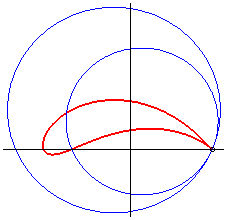
The Joukowski curves are the images of circles of the plane by the conformal map of Joukowski ; when the initial circle (C) passes by A(a,0) or A'(-a,0) (fixed points of the map), the Joukowski curve has a cuspidal point at A, and, in some cases, is an aerofoil.
The Joukowski transformation realises a conformal representation of the outside of the disk associated to (C) onto the outside of the curve, which enables to study the flowing problem around a plane wing with this shape by reducing it to the case of a circle.

Construction of the curve, using the initial curve and its image by the transformation .

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017