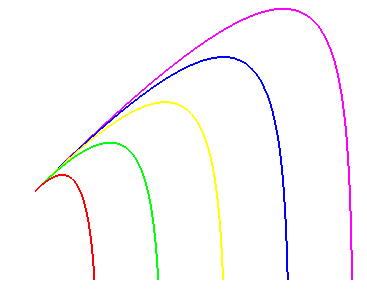
Fixed friction proportional to speed,
increasing initial speed, shooting angle of 60°
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BALLISTIC CURVE
|
Fixed friction proportional to speed, increasing initial speed, shooting angle of 60° |
|
|
| Curve studied by Jean Bernoulli in 1719, Euler in 1753, Legendre in 1782 and Jacobi in 1842. |
The ballistic curves are the trajectories of a massive point subject to a uniform gravitational field and a fluid friction force, in the opposite direction of the velocity vector, its intensity being proportional to a certain function j(v) of the absolute velocity.
1) When 
= 0, we get the parabola.
Differential equation of motion: 
where g is the gravitational acceleration.
Paramétrisation cartésienne : 
(condition initiale M(0) = 0, 
angle de tir initial).
Cartesian parametrization : |
 |
Distance from the starting point to the point of impact
on the ground :  ,
maximum for  .
Height reached :  ,
equals a/4 for .
Length of the trajectory : Opposite, view of different shots depending on the starting angle. |
 |
2) Case where
=
v (experimentally obtained for a low velocity; this resistance
is called "viscosity")
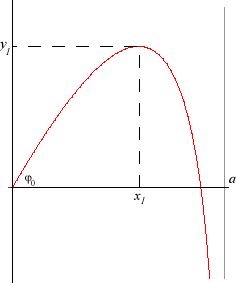
(Linear) differential equation of motion: 
( k = coefficient of friction).
Cartesian parametrization: 
(initial condition M(0) = 0) with  ,  , 
and  .
Cartesian equation:  .
Transcendental curve (as opposed to the parabola). |
 |
We get curves which, as opposed to the parabolas,
have a vertical asymptote at their right end, and an oblique asymptotic
branch without asymptote, at the left end.
| Opposite, figure composed of the trajectories starting from a fixed point with constant initial speed, shooting angle of 45°, and an increasing friction coefficient. |  |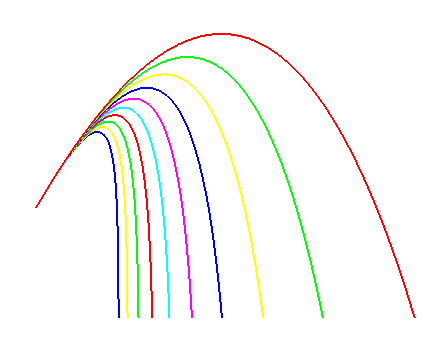
| Figure composed of the trajectories starting from a fixed
point with given initial speed, along with the envelope
of these trajectories (called safety parabola even though it is not a parabola).
Compare to the case without friction. |
 |
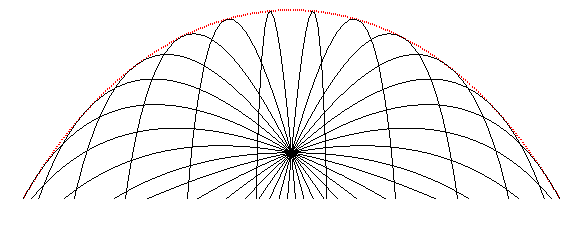Remark: the Cartesian equation of these curves shows that they are the medians of a line and a logarithmic curve, along the asymptote of the logarithmic curve.
3) General case.
Differential equation of motion: 
which can be written: 
hence  ,
so that, with  ,  :
differential
equation giving 
as a function of u. Substitution of
into (1) gives 
hence, using  ,
the parametrization of the curve as a function of u. |
| Opposite, comparison between 3 ballistic curves, under
the same shooting angle and with the same initial speed:
- in blue, in space
|
 |
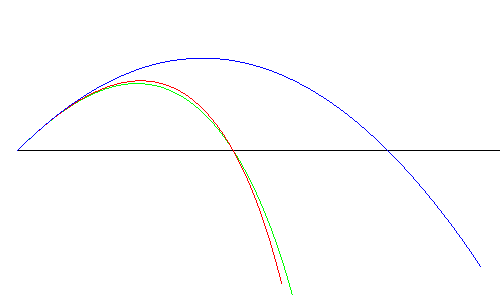| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
with 
.
,
equals a(sqrt(2) + ln(1 + sqrt(2)))/2 = 1,15
a (OEIS : 
, 
(
inverse
of the