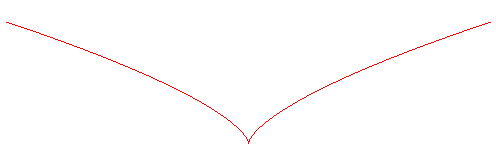
SEMICUBICAL PARABOLA
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SEMICUBICAL PARABOLA

| Curve studied by Neile
in 1657, Leibniz in 1697 and Newton in 1701.
Other name: Neile parabola. |
 |
Cartesian equation: Cartesian parametrization: Polar equation: Curvilinear abscissa: Polynomialcubic with a cuspidal point. |
The semicubical parabola is a divergent
parabola in the case where the polynomial P has a triple root.
It is the evolute
of the parabola, and the pedal
of the cissoid of Diocles.
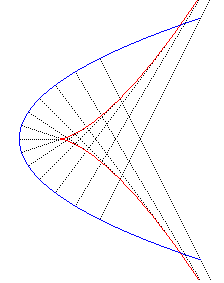
Contrary to the parabola, the semicubical parabola can be parametrized by the curvilinear abscissa using rational functions.
The semicubical parabola possesses the important property of being an isochronous curve: see isochronous curve of Leibniz.
The surface generated by revolution of the curve around
its axis is the neiloid.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017