Complex parametrization:  where a is the radius of the base circle, that of the rolling circle (q > 1), and d the distance between the point and the centre of the moving circle.

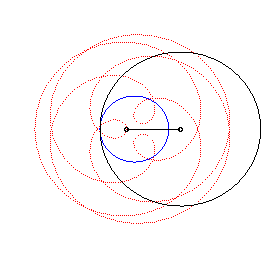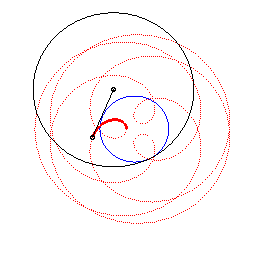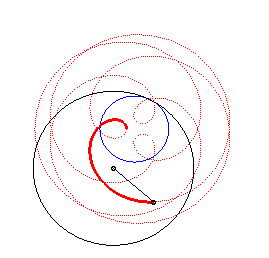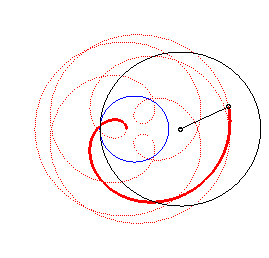
The peritrochoids are the curves described by a point linked to a circle rolling without slipping on a base circle (C₀), while containing this circle. In other words, they are the roulettes of a motion of a plane over a fixed plane the base of which is a circle and the rolling curve of which is a circle containing the first circle.

This curve is in fact an epitrochoid  (base circle with radius , rolling circle with radius with , distance between the point and the centre of the rolling circle).

The notion of peritrochoid differs from that of epitrochoid only by the generation of the curve, not by the curve itself, so we refer the reader to epitrochoid for a complete study.
 
 

The hull of the Wankel motor has, by construction, the shape of a peritrochoid (click on the image for the animation).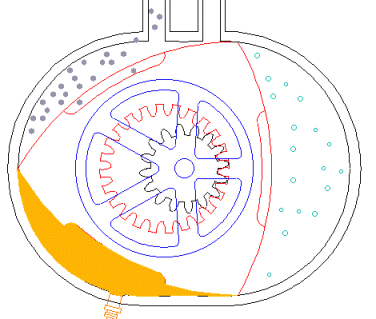

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017