PEDAL OF A CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PEDAL OF A CURVE
| Notion studied by Roberval in 1693, Maclaurin in 1718,
Steiner in 1840, Terquem, who named it, in 1847.
From the Greek, pous, podos "foot". |
If M0 is the current
point on  ,
then the current point M on the pedal is defined by  ,
which gives:
in Cartesian coordinates, 
in complex parametrization, and
in polar coordinates, with  ;
we thus have 
(see the notations).
If the tangential equation of
is f(u, v, w) = 0 (which means f(u, v, w) =
0 is a condition for the line 
to be tangent to (G0)),
then the polar equation of the pedal with respect to O is 
and its Cartesian equation is  .
If the polar equation of the curve
is  , then
the polar equation of its pedal is  . |
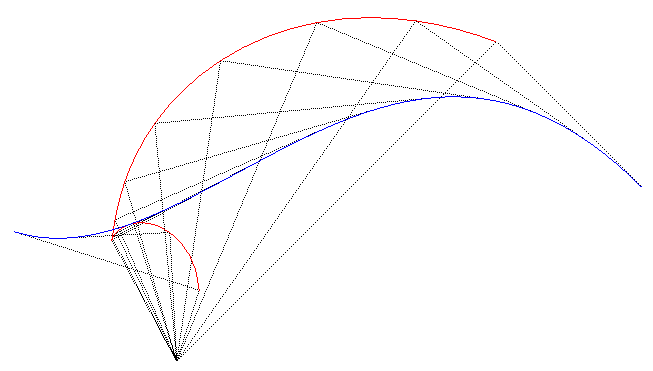
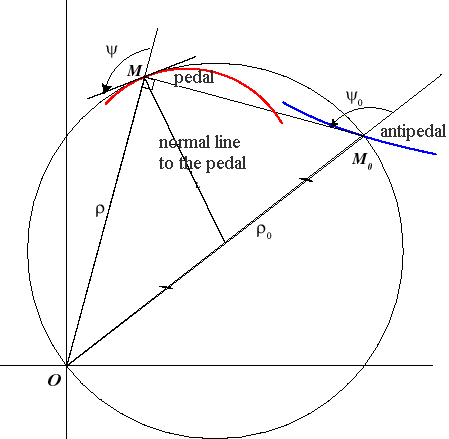
The pedal of a curve
with respect to a point O (or with pole O) is the locus of
the feet of the lines passing by O perpendicular to the tangents
to the curve .
| Therefore, it is also the envelope of the circles with
diameter [OM0], when M0describes
(this property provides a construction of the normal, and therefore of
the tangent to the pedal). |
Prove that ! |
Finally, it is the inverse,
with any circle with centre O as reference circle, of the polar
of with
respect to this circle.
The pedal is the homothetic image of the orthotomic.
The curve the pedal of which is a given curve is called the negative pedal.
Examples:
- The pedals of parabolas with respect to a point
different from the focus, the cissoids
of a circle and a line with respect to a point on the circle, and the set
of the rational
circular cubics coincide. More precisely: the pedal with respect to
O
of the parabola with focus F and tangent at the vertex (T)
is the cissoid with pole O of the circle with diameter [OF]
and the line (D), image of (T) by the translation of 
.
- The pedals of centred conics, the cissoids
of two circles with respect to a point on one of them, and the set of the
rational
bicircular quartics coincide.
Other examples regrouped in a table:
| negative pedal
(or orthocaustic) |
pole (position with respect to the negative pedal) | pole (position with respect to the pedal) | pedal |
| line | any point | any point | point (projection of the pole on the line) |
| parabola | focus | outside the line | line (tangent at the vertex of the parabola) |
| " | different from the focus | singularity | rational circular cubic |
| " | inside the parabola | isolated point | acnodal rational circular cubic |
| " | on the internal part of the axis of the parabola | Sluze cubic | |
| " | at the middle of the segment line [SF] | isolated point | visiera |
| " | on the parabola | cuspidal point | cissoid |
| " | at the vertex | cuspidal point | cissoid of Diocles |
| " | outside the parabola | double point | crunodal rational circular cubic |
| " | on the tangent at the vertex | double point | ophiuroid |
| " | on the directrix | double point | strophoid |
| " | foot of the directrix | double point | right strophoid |
| " | symmetric image of the focus about the directrix | double point | Maclaurin trisectrix |
| centred conic | focus | outside the circle | (principal) circle (of the conic) |
| " | different from the focus | real singularity | rational bicircular quartic |
| " | centre | real singularity | Booth curve |
| circle | outside the circle | double point | limaçon of Pascal with a loop |
| " | on the circle | cuspidal point | cardioid |
| " | inside the circle | isolated point | limaçon of Pascal without a loop |
| " | centre | centre | same circle |
| rectangular hyperbola | centre | double point | lemniscate of Bernoulli |
| Tschirnhausen cubic | focus (at the 8/9-th of the segment line [double point, vertex]) | focus | parabola |
| cissoid of Diocles | point with coordinates (4a, 0) | vertex | cardioid |
| cardioid | cuspidal point | vertex of the loop | Cayley sextic |
| cardioid | centre of the conchoidal circle | vertex of the loop | trisectrix limaçon |
| cardioid | point with coordinates (-a,0) | triple point | nephroid of Freeth |
| deltoid | any point | folium | |
| deltoid | inside the deltoid | trifolium | |
| deltoid | on a symmetry axis of the deltoid | right folium | |
| deltoid | on the deltoid | bifolium | |
| deltoid | centre | regular trifolium | |
| deltoid | cuspidal point | simple folium | |
| deltoid | vertex | regular bifolium | |
| centred cycloid | centre | centre | rose |
| astroid | any point | beetle | |
| astroid | centre | centre | rose with four branches |
| paracycloid | centre of the frame | pole | spiral  |
| hypercycloid | centre of the frame | pole | spiral  |
| sinusoidal spiral with parameter n = –1/m | centre | centre | sinusoidal spiral with parameter n/(n+1) = –1/(m–1) |
| logarithmic spiral | centre | centre | logarithmic spiral |
| involute of a circle | centre | centre | Archimedean spiral |
| hyperbolic spiral | centre | centre | tractrix spiral |
| Norwich spiral | centre | centre | Galilean spiral |
| Maltese cross | centre | centre | double egg |
| Talbot curve | centre | centre | ellipse |
| evolute of a centred conic | focus | Jerabek curve |
| Let us state the beautiful Steiner-Habich theorem:
If a curve (C) rolls on a line (D), and if (R) is the roulette described by a point M of the plane of this curve, then a copy of the pedal (P) of (C) with respect to M can roll on (R), in such a way that the point M describes the line (D). Then, the couple ((R), (P)) is a wheel-road couple. See many examples on the latter link. |
The contrapedal of (G0)
with respect to O can be defined as the locus of the feet of the
lines passing by O perpendicular to the normals to .
The contrapedal is then none other than the evolute.
See also the pedal
surfaces.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017