


| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PARALLEL PURSUIT CURVE
The notion of parallel pursuit curve refers to the trajectory of a moving point M (the chaser) following another moving point M0
(the fugitive) in such a way that the line (M0M) (the vision line) remains parallel to itself as time goes by.
It is a limit case of shadowing curve, when the "tree" is placed at infinity.
The problem has a determined solution if a condition on the speed of M is imposed. We will consider here the case where the speeds V and V0 of M and M0 are proportional (V= kV0): the pursuit curve obtained does not depend on the speed profile of the fugitive.
Then, the notion is involutory, in the sense that the escape curve is a pursuit curve associated to the initial pursuit curve, if k is replaced by 1/k.
| For k = 1 (chaser and fugitive have the same speed), the motion of the chaser (2 possibilities in red opposite) is the symmetric or translated image of that of the fugitive. |
 |
| For k > 1, there still are two symmetric solutions for the chaser, one of which still catches the fugitive (the only one we will consider from now on). |  |
| For k <1, there isn't always a solution, or the solution might only exist during a certain period of time, see opposite. |  |
| Conditions imposed on the motion of the chaser, in Cartesian coordinates: Solution in a special case covering the generality: at the time t = 0, the chaser is at O and the fugitive on the axis Ox; if the motion of the fugitive is parametrized by (so there are two symmetric solutions about Oy) |
Some special cases:
1) The motion of the fugitive is linear.
Then, the parallel pursuit curve is, if it exists, also linear.
| Motion of the fugitive: |
Motion of the chaser: |
Collision time: |
| When k > 1 the chaser always catches the fugitive; example opposite with |
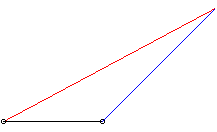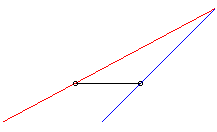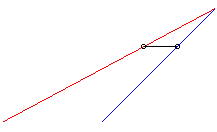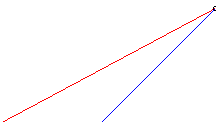 |
| When k |
 |
REMARK: in that case, the parallel pursuit curve is in fact the intelligent dog curve, who, instead of running, at every instant, in the direction of its master, goes straight to the point where, given its speed and that of the master, it will meet them in a straight line. In the case where the fugitive follows any given trajectory, a parallel navigation consists in always taking the direction of the intelligent dog, and supposing that the fugitive will stay on a straight line. This optimises the catching of the fugitive by the chaser; the optimum being, of course, the seer curve, who would always guess the movement of the fugitive and determine the direction to take to meet them on a straight line.
2) The motion of the fugitive is circular.
| Motion of the fugitive: |
Motion of the chaser: |

Example with k = 1.5 and a = 2b |

Comparison with the classic pursuit curve |
The simple pursuit and the parallel pursuit are special cases of the pursuit called "proportional navigation"; in that case, the speed of rotation of the vision line is proportional to that of the velocity vector of the chaser. If the ratio is k, then the limit case k = 0 corresponds to the parallel pursuit, and the case k = 1 corresponds to the simple pursuit (if the chaser takes the direction of the fugitive at the initial time).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017