RATIONAL BICIRCULAR QUARTIC
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RATIONAL BICIRCULAR QUARTIC

| Polar equation: Cartesian equation: Case |
The rational bicircular quartics are the bicircular quartics with a real singularity - here, O- that is necessarily unique (the cyclic points are the other two singularities); the quartic is called crunodal, cuspidal, or acnodal, depending on whether this singularity is a double point with different tangents, a cuspidal point, or an isolated point.
Like the rational circular cubics, they have the property of having 4 equivalent remarkable geometrical definitions.
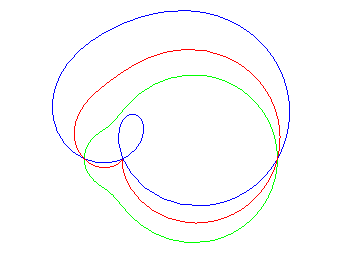
1) They are the pedals
of centred conics (here pedal with respect to O of the conic ).
They are crunodal, cuspidal, or acnodal depending on
whether the point O is outside, on, or inside the conic.
crunodal case |
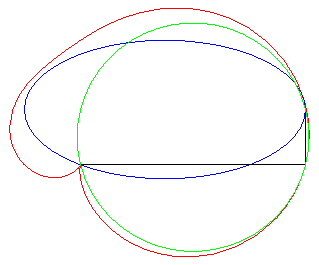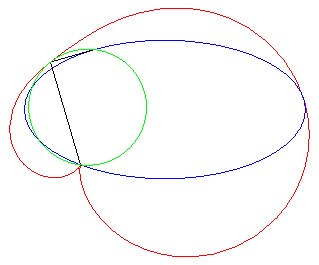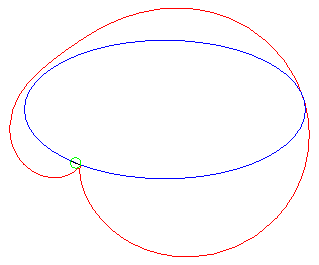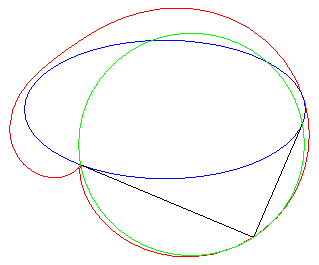
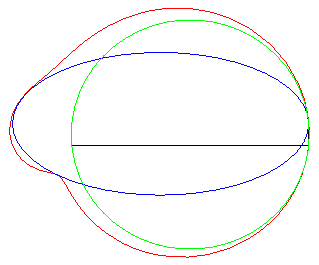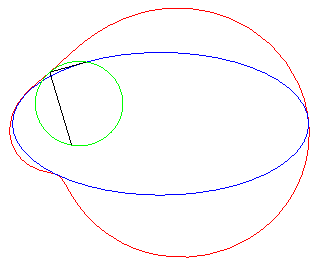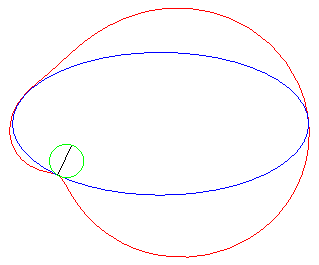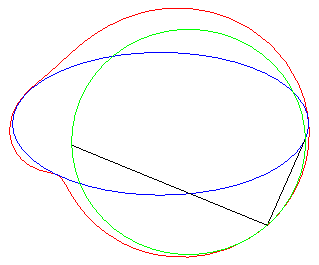
cuspidal case |
acnodal case |
Examples: when the conic is a circle, we get the limaçons of Pascal (including the cardioid) and when O is the centre of the conic, we get the Booth curves (including the lemniscate of Bernoulli).
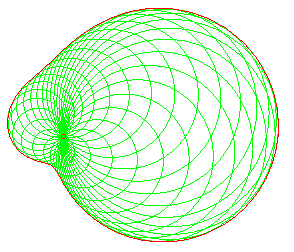
This definition as a pedal implies a definition as the roulette of a conic rolling on an equal conic, and also as a curve of the three-bar linkage in the case of the antiparallelogram.
 tracing
of a point on an ellipse rolling on an equal ellipse: we get a pseudo-cardioid.
tracing
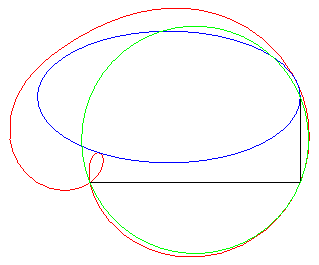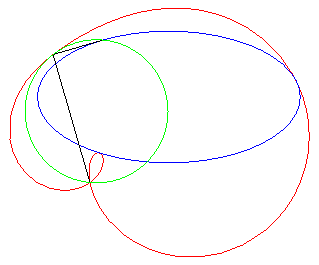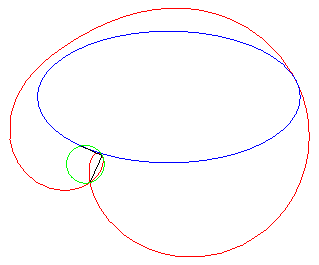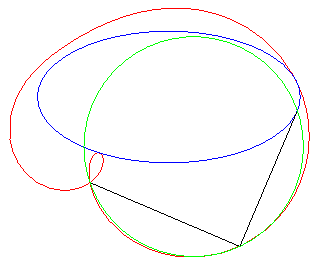
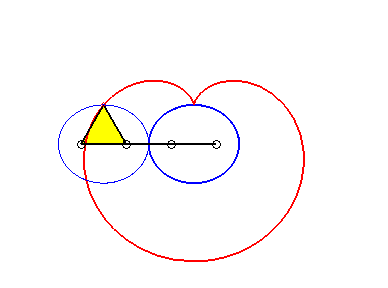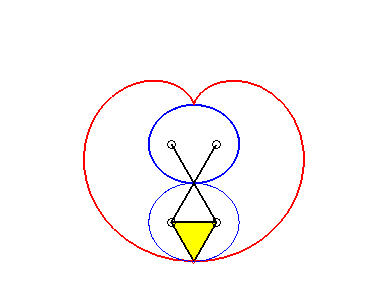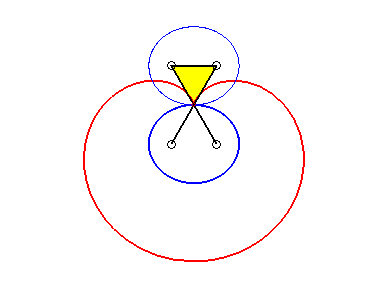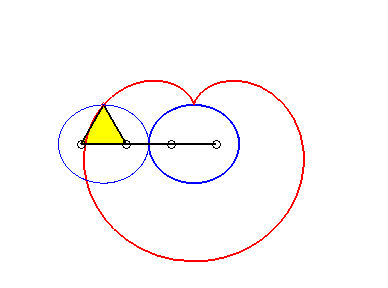
of a point on an ellipse rolling on an equal ellipse: we get a pseudo-cardioid.2) They are the envelopes of the circles with diameters
the ends of which are a fixed point (here O) and a point describing
a centred conic.

crunodal case |

cuspidal case |
acnodal case |
3) They are the inverses
of conics with respect to a point that is not on the conic (here, the conic
with equation:
where p is the square of the inversion radius).
The quartic is crunodal, cuspidal, or acnodal depending
on whether the conic is a hyperbola, a parabola or an ellipse.
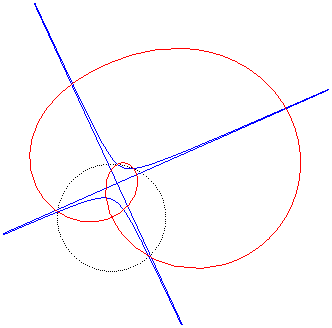
crunodal case |

cuspidal case |
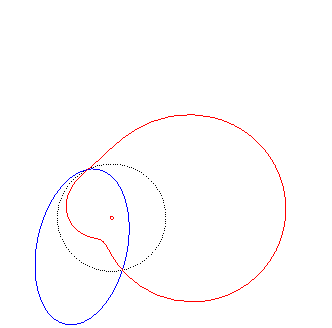
acnodal case |
4) They are the cissoids
of two circles with respect to one of the points of one of these circles,
the first one being the circle with centre
passing by O and the second one being the circle with centre
and radius a. The quartic is crunodal, cuspidal, or acnodal depending
on whether these circles intersect, are tangent or are disjoint.
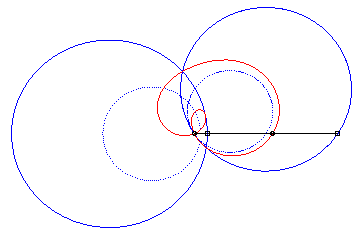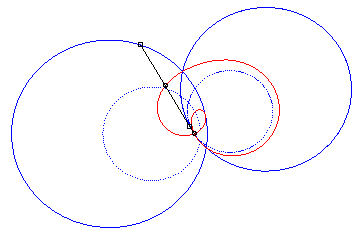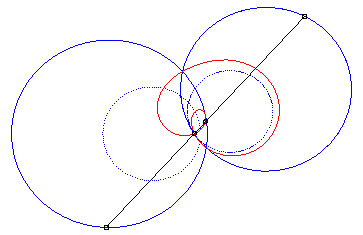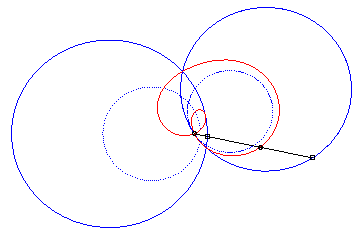
crunodal case |
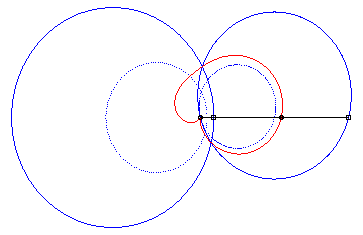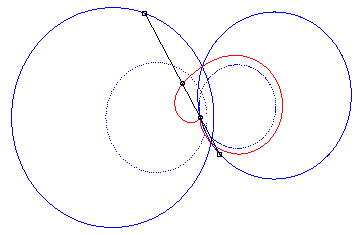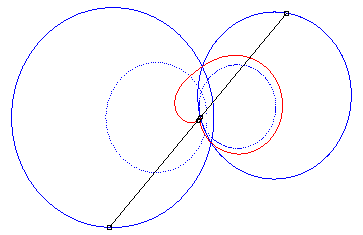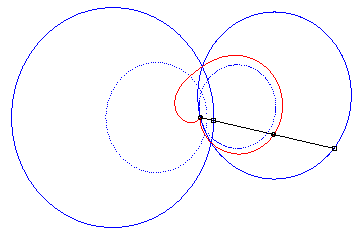
cuspidal case |
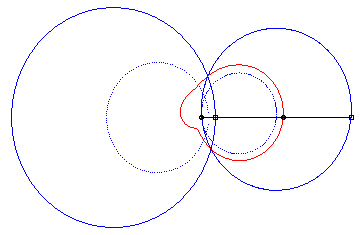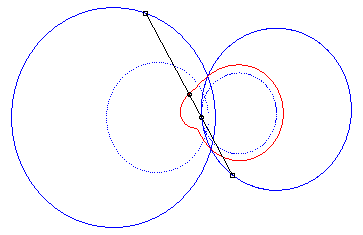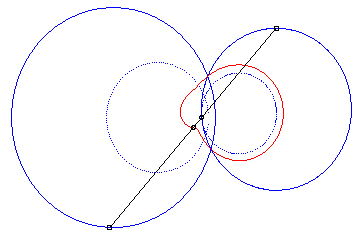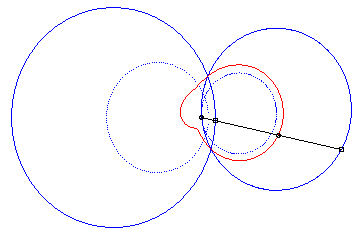
acnodal case |
See also, as a special case, the Dürer
conchoid.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017