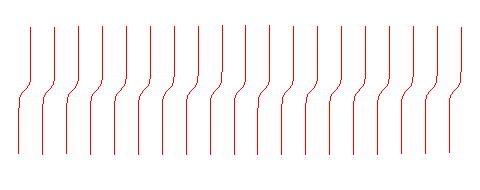
Curve studied by Wilhelm Nördling in 1867, L. Fargue in 1868, Emile Turrière in 1939. See this article on railways, from which the above figure is taken.

The radioids are the curves that allow to connect a segment of a line to an arc of a circle, so that the curvature varies continuously, with the final aim of applications in railways and roads: the passenger of a vehicle moving along this curve will be subject to a centrifugal force that also varies continuously, which is not the case for a curve composed of a segment line and an arc of a circle.

Any curve of class C² with a point with zero curvature can be called a radioid, but, in practice, the following curves were used:

    - the elastic curve  (radioid with curvature proportional to the abscissa)
    - the cubical parabola or Nördling parabola: y = x³ that approximates the previous one around the inflection point
    - the clothoid (radioid with curvature proportional to the curvilinear abscissa)
    - the Norwich spiral (radioid with curvature proportional to the distance to a fixed point)
    - the pseudo-elliptic radioid, studied below

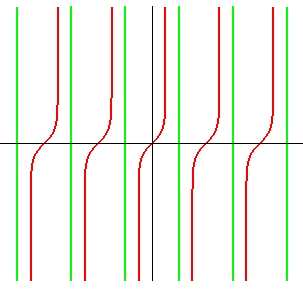Cartesian equation:  which, when , can be written under the equivalent forms: y = a gd-1 (x/a) = ln (tan(x/2a + p/4)) = argsinh(tan x/a) = argtanh(sin x/a) = sign(x).argcosh(sec(x/a)), where gd-1 is the inverse Gudermannian function. Transcendental curve. Cartesian parametrization: . Cartesian tangential angle: . Curvilinear abscissa:  (pseudo-elliptic integral, hence the name of the curve), where . Curvature: .

The pseudo-elliptic radioid is the plot of the inverse Gudermannian function. It looks like the tangentoid, but it is interesting because of the fact that its curvilinear abscissa can be calculated thanks to usual functions, and not thanks to elliptic functions, like the curvilinear abscissa of the tangentoid.
It is the curve of a rhumb line of the sphere in geographic coordinates.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017