BEETLE CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BEETLE CURVE
| Curve found under this name in 1857 in the textbook of Ecole polytechnique applicants, redacted by Catalan, and then in the treatise on analysis of Laurent. |
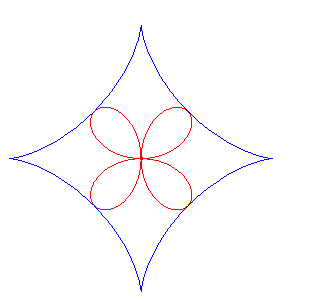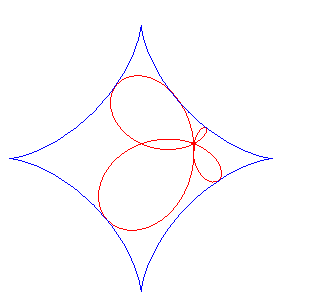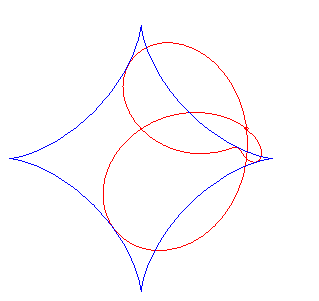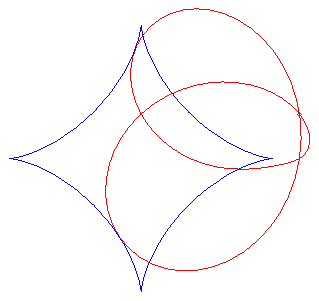
Polar equation:  .
Cartesian equation:  .
Polar equation in the case a = b, in a frame turned by p/2:  .
Rational sextic. |
The beetle curves are the pedals of astroids;
here, the point O is the pole of the pedal, and the centre of the
astroid is A(a, b), and its parametrization is 
.
The polar equation shows that the beetle curves are the
cissoids
of the circle and the quatrefoil;
and, besides, we get this trefoil when
a = b = 0.
The beetle curves are to the astroid what the folia
are to the deltoid.
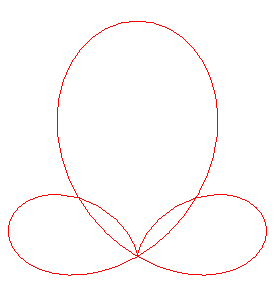
case |
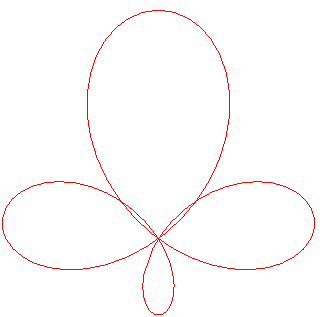
case  |
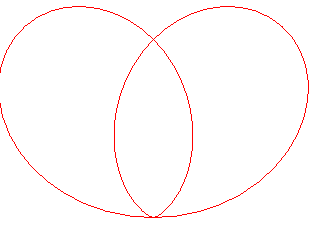
case a = 0, b = r, equation |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL2017
