Maclaurin sectrix

MACLAURIN SECTRIX

Curve studied by Maclaurin in 1742, Plateau in 1828 and Kempe in 1895.
Colin Maclaurin (1698-1746): Scottish mathematician.
Other names: Plateau sectrix, isocyclotomic curve, spider (Heymann 1899).
Loria p. 460.

The Maclaurin sectrices are the loci of the intersection point between two lines each in uniform rotation around a fixed point.

Given the fixed point O and A(a, 0), if the angular speed of the line D_A passing by A is equal to k times that of the line D₀ passing by O, then we get:
Polar equation in the frame with pole O: , being the angle when D_O passes by A.
Polar equation in the frame with pole A: .
We get all the sectrices by assuming |k| > 1 (swapping O and A amounts to changing k into 1/k).

The two inverses of a Maclaurin sectrix with respect to the 2 poles are still Maclaurin sectrices: the inverse of with respect to O is , and the inverse of with respect to A is .

When has a ruler-and-compass construction and when k is an integer, the Maclaurin sectrix is a |k|-sectrix, since the ratio between the angles is constant equal to k. And it is also a |k–1|-sectrix since .

Remarkable special cases for = 0 (i.e. when, at some point during their motion, the two lines coincide):

k= equation with pole O equation with pole A name of the curve figure remark

2 (or 1/2) circle 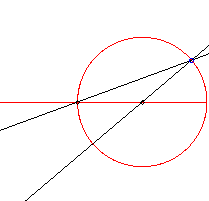This is equivalent to the central angle theorem.
What is the curve described by the intersection point of the two lines passing by the seconds hands of two watches places in the same plane?

-1 line 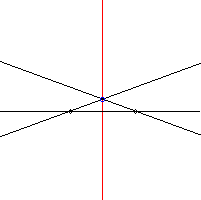The bisector of an isosceles triangle is also its mediatrix!

3 (or 1/3) Maclaurin trisectrix

3/2 (or 2/3) trisectrix limaçon

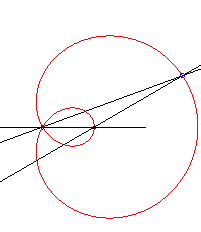-2 (or -1/2) hyperbola with eccentricity 2

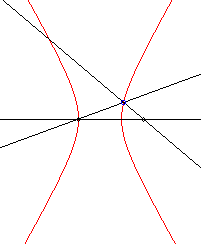Note that among the 3 curves , each one is the inverse of the other two (the case k = 3 gives the 3 previous curves).

Special cases with :

k = 1 circle 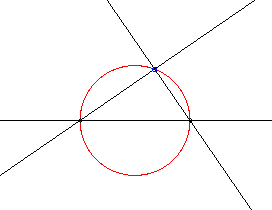Remark: this is equivalent to the inscribed angle theorem

k = 2 right strophoid

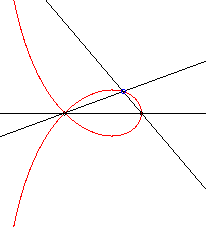k = - 1 rectangular hyperbola

Other examples:

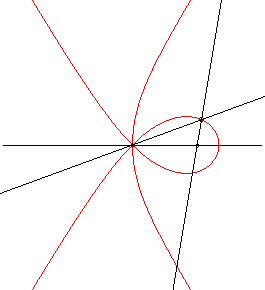
k = 4, q₀ = 0; it is also a trisectrix curve (cf. the remark above).
k = 3, q₀ = p/2

The limit case where one of the poles is at infinity is none other than that of the Dinostrate quadratrix and its generalisations.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

k=	equation with pole O	equation with pole A	name of the curve	figure	remark
2 (or 1/2)			circle		This is equivalent to the central angle theorem. What is the curve described by the intersection point of the two lines passing by the seconds hands of two watches places in the same plane?
-1			line		The bisector of an isosceles triangle is also its mediatrix!
3 (or 1/3)			Maclaurin trisectrix
3/2 (or 2/3)			trisectrix limaçon
-2 (or -1/2)			hyperbola with eccentricity 2

k = 1	circle	Remark: this is equivalent to the inscribed angle theorem
k = 2	right strophoid
k = - 1	rectangular hyperbola