Curve studied by Lucas in 1879.[brocard partie comp. , loria p521]

 

Multipolar equation: . Algebraic curve of degree 2n. The stelloids and the Cassinian curves are the inverse images of the coordinate lines by the complex function f defined by .

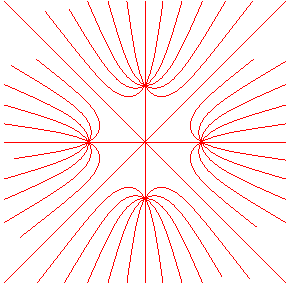
Given n fixed points on the plane, the stelloids with pole the s are the loci of the points M of the plane such that the mean of the angles formed by the lines and a fixed direction, is constant. The curves do not depend on the chosen fixed direction.

The stelloids are none other than the orthogonal trajectories of the Cassinian curves with same poles.

The case n = 2 gives the rectangular hyperbola, orthogonal trajectory of the Cassinian ovals.

The equipotential lines of the magnetic field created by n parallel wires carrying a current with same intensity and in the same direction are, in any plane orthogonal to the wires, the stelloids with foci the intersection points with the wires; ditto for the field lines of the electrostatic field created by n uniformly charged parallel wires with identical charges.

These curves can be generalised to weighted means, in other words, to a multipolar equation of the type: ; these curves can be physically obtained as the equipotential lines of magnetic fields with wires carrying distinct currents, or as electrostatic field lines with wires bearing different charges.

For example, with n = 2 et , we get a pencil of circles with base points the poles.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017