Stophoidal curve

STROPHOIDAL CURVE

From the Greek strophos "string, belt, braid".

For an initial curve with polar equation in the frame (F, , ) and a point O with coordinates (a, b) in this frame:
Polar equation in this frame: .

The strophoid (or strophoidal curve) of a curve with respect to thepole O and fixed point F is the locus of the points M on a variable line (D) passing by O such that M₀M = M₀O where M₀ is an intersection point (different from F) between the line (D) and the curve .
In other words, it is the locus of the intersection points between a circle centred on M₀ on the curve and passing by O, and the line (FM₀).
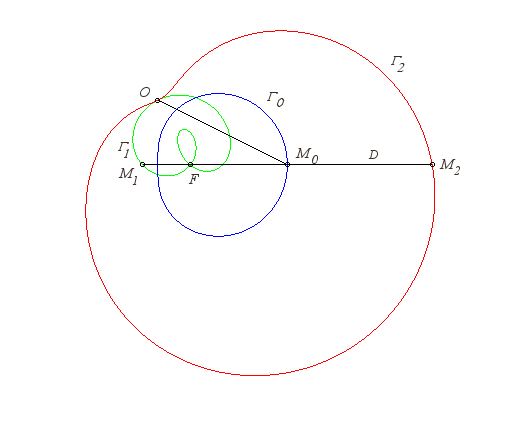
The strophoidal is therefore composed of two branches and the median with pole O of which is .
M₀M₁=M₀M₂ = M₀F

When the curve is a line, O a point on this line and F a point outside this line, the corresponding strophoidal curves are the strophoids (right strophoids when (OF) is perpendicular to the line ).

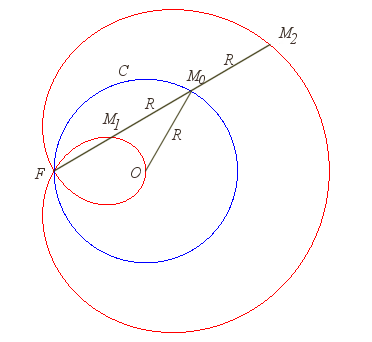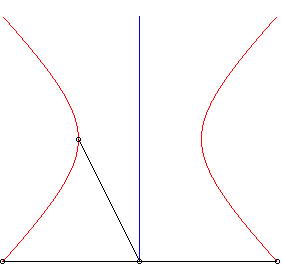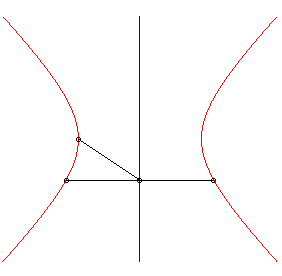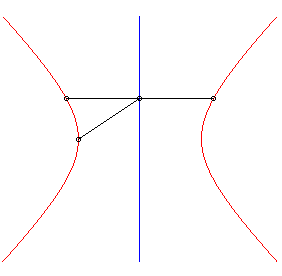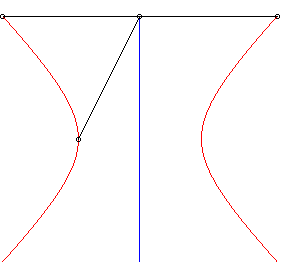
When the curve is a circle, O its centre, the strophoid is the conchoid of with pole O and modulus the radius of the circle; in particular, when O is on the circle, we get the trisectrix limaçon.

Construction of the strophoid of a circle, in the case where O is on the circle and O, F and the centre of the circle are aligned.
When F is on the centre of the circle, the strophoid is Freeth's nephroid. When F goes to infinity, the strophoid goes to a torpedo (see below).

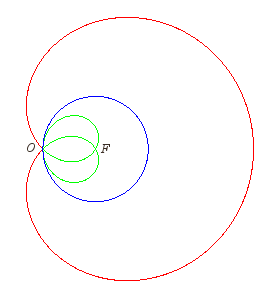Lorsque F est diamétralement opposé à O, la strophoïdale se réduit à deux cercles, centrés sur le cercle de départ, et de rayon (à justifier géométriquement !).

GENERALISATIONS

1) The point F is placed at infinity.

The strophoidal curve of a curve with respect to a pole O and a line direction D is the locus of the intersection points between a circle centred on M₀ on the curve and passing by O, and the line parallel to D passing by M₀.
The associated transformation is sometimes called "Brocard transformation", since he studied it in the special case of a circle.

For a line direction Ox and for an initial curve with polar equation in the frame (O, , ): , the strophoidal curve is the reunion of the two curves with polar equation and .
Opposite, construction of one of the two branches.

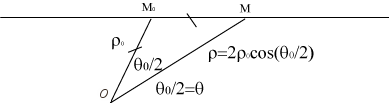Examples:

When the curve is a line, and O a point outside this line, we get the hyperbolas (see opposite the case where the line is perpendicular to (Ox)).

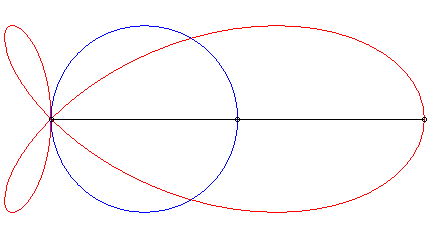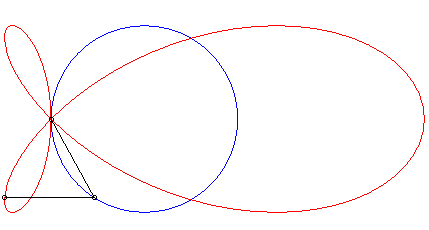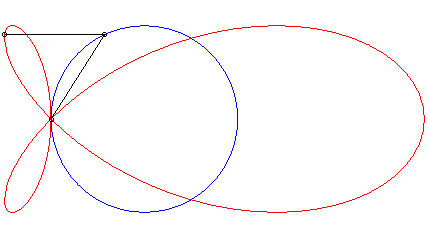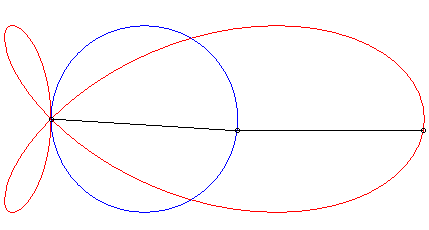When the curve is a circle, and O a point on that circle (equation ), the strophoidal curve is the trifolium: . See opposite the case where the circle is centred on Ox, which gives the torpedo. When the circle is centred on Fy, we get the regular bifolium.

When the initial curve is a parabola with focus O and parameter p, and the line direction is the axis of the parabola, one of the branches of the strophoidal curve is none other than the directrix while the other branch is a parabola with vertex O and parameter p/2.

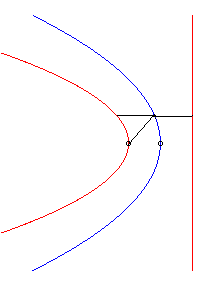When the initial curve is an ellipse with focus O and the line direction is an axis of the ellipse, then the strophoidal curve is composed of two other ellipses, with summits O.
A similar phenomenon occurs for the hyperbolas.

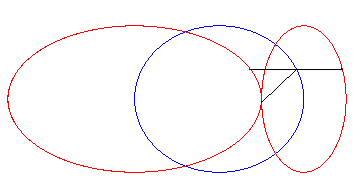When the initial curve is a hyperbolic spiral , the strophoid "on the right" is a syncochleoid , and that "on the left" (in green), a cochleoid .

2) The point O is replaced by a curve (idea of Pierre Daniel).

The strophoidal curve of a curve with respect to a curve and a fixed point F is the locus of the intersection points between a circle centred on M₀ on the curve and tangent to the curve , and the line (FM₀).

Here is a simple special case: the curve is a line passing by F.

With the axis Fy as the line and , with polar equation in the frame (F, , ) , as the initial curve, the polar equation of the strophoid is .
Opposite, the example of the parabola ; the equation of the strophoid is ; it is a focal conchoid of the parabola .

Another example:

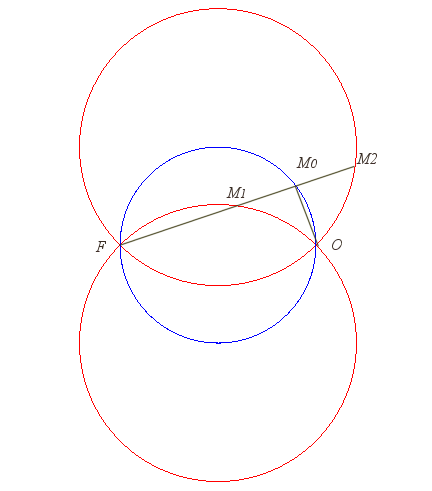
The strophoidal curve of an ellipse (C) with fised point one of its foci F, with respect its directrix circle centred on F, is composed of the directrix circle itself and the conchoid with pole F and parameter 2a of the image of the ellipse by the homothety with centre F and ratio 2 (indeed, with the notations of the figure:
FS = FC – CP = 2FC – 2a = FC' – 2a.).
This strophoid is therefore a Jerabek curve.
The same phenomenon occurs in the case of a hyperbola.

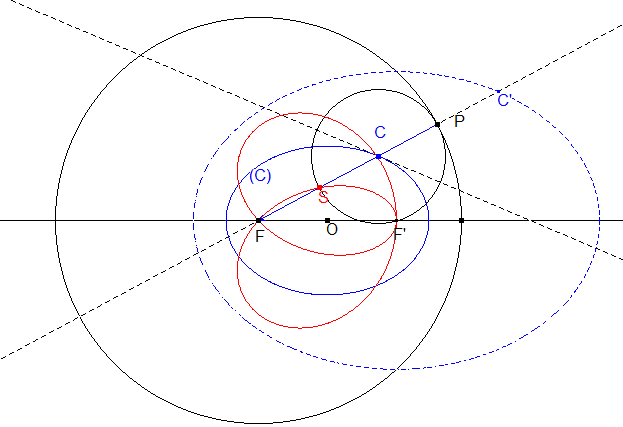next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

When the curve is a line, and O a point outside this line, we get the hyperbolas (see opposite the case where the line is perpendicular to (Ox)).
When the curve is a circle, and O a point on that circle (equation ), the strophoidal curve is the trifolium: . See opposite the case where the circle is centred on Ox, which gives the torpedo. When the circle is centred on Fy, we get the regular bifolium.
When the initial curve is a parabola with focus O and parameter p, and the line direction is the axis of the parabola, one of the branches of the strophoidal curve is none other than the directrix while the other branch is a parabola with vertex O and parameter p/2.
When the initial curve is an ellipse with focus O and the line direction is an axis of the ellipse, then the strophoidal curve is composed of two other ellipses, with summits O. A similar phenomenon occurs for the hyperbolas.
When the initial curve is a hyperbolic spiral , the strophoid "on the right" is a syncochleoid , and that "on the left" (in green), a cochleoid .