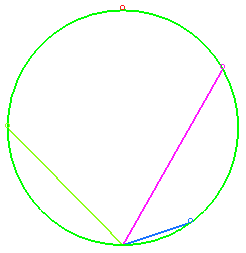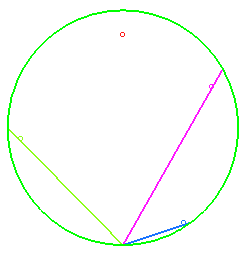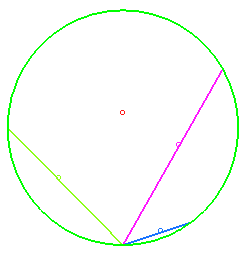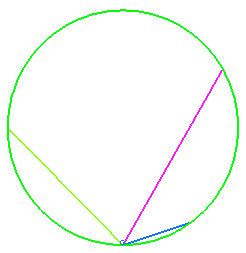
Given a family of secant lines O placed in a uniform gravitational field, and massive points sliding without friction on each of these curves, Galileo posed the problem of determining on which curves the points had to be in order to, with no initial speed, arrive simultaneously at O; the answer is a circle the bottommost point of which is O.

O

We derive from this that if all the points leave O with no initial speed on lines passing by O, then the curve they generate at every instant is also a circle.

If the lines are replaced by a family of curves passing by O, with the condition that the points have to pass simultaneously by O, then the curve they generate at every instant is called synchronous curve.

Example:
If the curves are cycloids with horizontal base and cuspidal point at O, the points leaving O with no initial speed, then the synchronous curves are the orthogonal trajectories of these cycloids (Jean Bernoulli).

See also synodal curve, isochronous curve of Huygens, isochronous curve of Leibniz, isochrononous curve of Varignon, brachistochrone and tautochronous curve.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017