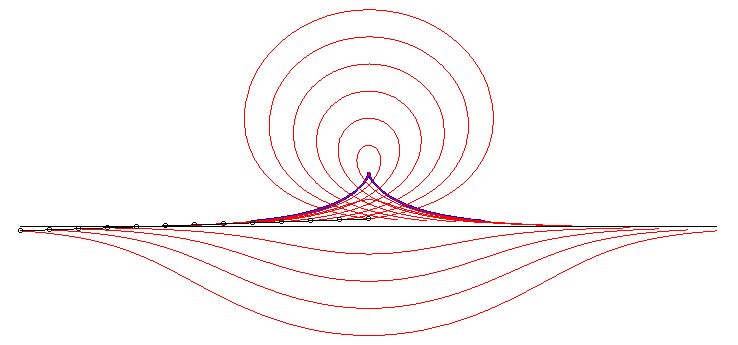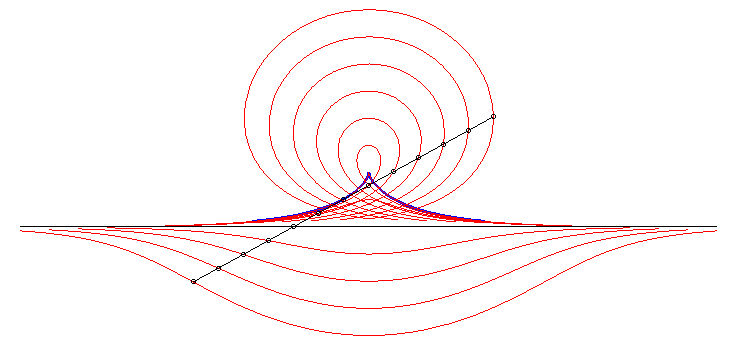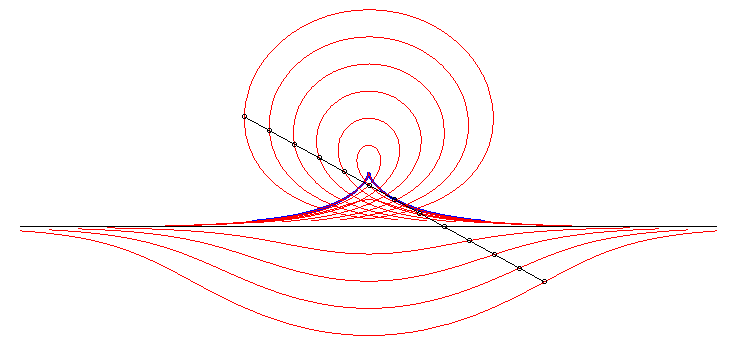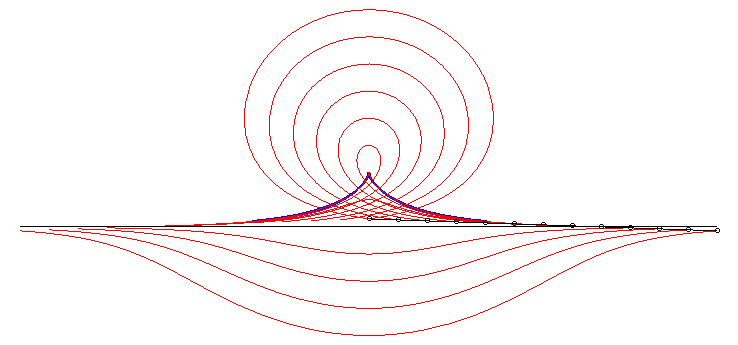
Cartesian parametrization , the cases k = 0 , k = 1 et k = 2 correspond, respectively, to the line, the tractrix, and the convict's curve. Curvilinear abscissa:  (therefore, s = at in the case of the convict's curve). Radius of curvature: . Hence the intrinsic equation 1 in the case of the convict's curve:

The syntractrices are the curves described by the points of a tangent to the tractrix.

If the point N describes the tractrix, and P is the point on the tangent at N located on the asymptote to the tractrix (we know that NP = a = constant), then the above parametrization is that of the point M such that .
 
 

When N is the middle of [PM] (i.e. k = 2), the curve is called convict's curve, which is also a special case of elastic curve. Here is a possible explanation for this name: A very heavy wagon is located at N, middle of a fixed rod MP; a first convict is at P and pulls the wagon N along a line; the wagon therefore describes a tractrix; a second convict pushes at M and therefore describes the convict's curve. More generally, when the front wheels of a vehicle describe a line, then the various points on its symmetry axis describe syntractrices.

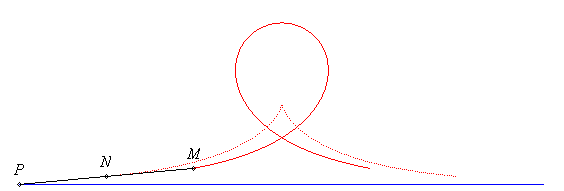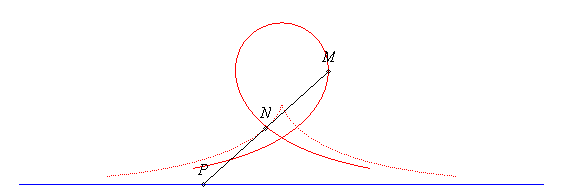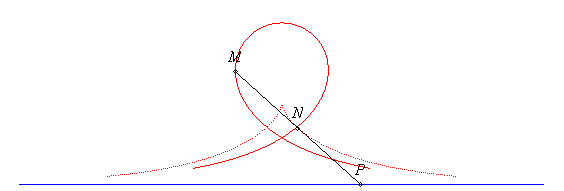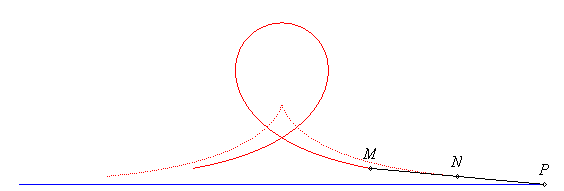
The calculation of the curvilinear abscissa above shows that the convict's curve is the curve that the end of a rod must describe, when the other one has a linear motion, so that the two ends (P and M) have the same absolute speed.

 

The convict's curve is the median along Ox of the semicircle  and the tractrix .

 
 

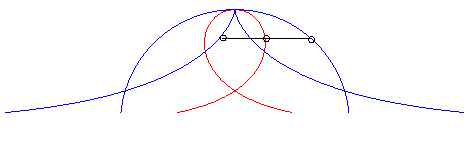The convict's curve is also the special case k = 2 of the family of curves with intrinsic equation 1:, curves that do not have a given name, but are parametrized by:  Opposite, an animation for k ranging from 0 to 6, with stops for k =1 (catenary of equal strength), k = 2 (convict's curve), and k = 4.

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2021