TALBOT CURVE

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TALBOT CURVE

| Curve studied by Roche and Talbot in 1821, then by Tortolini in 1846. |
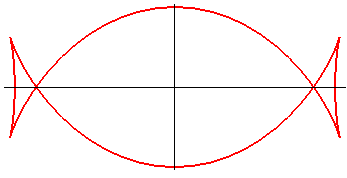 |
Cartesian parametrization, starting from the ellipse 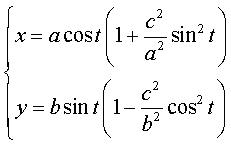
where Rational sextic. |
The Talbot curve is the negative pedal of the ellipse with respect to its centre. It is therefore the envelope of the lines perpendicular to the diameters of the ellipse, at their ends.

for |
|
| Therefore, the Talbot curve is also (up to homothety with ratio 1/2), the isotel of the ellipse with respect to its centre, i.e. the locus of the centres of the circles tangent to the ellipse and passing by its centre. |
|
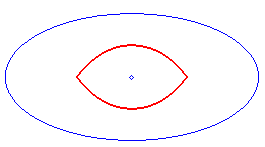 |
| This curve can be generalised by considering the negative pedal of the ellipse with respect to any point on its major axis, located at distance d from the centre.
We get the parametrization: |
|
|
First special case: negative pedal of the ellipse with respect to a focus (d = c). The first parametrization simplifies to The case |
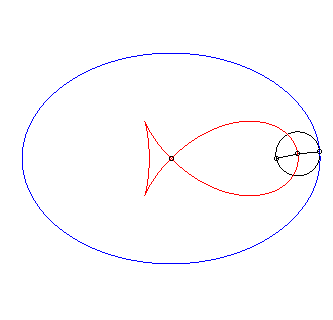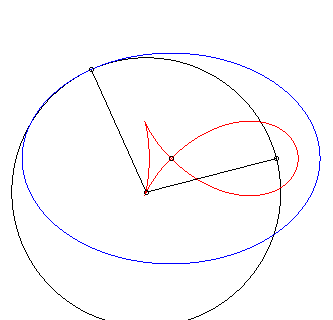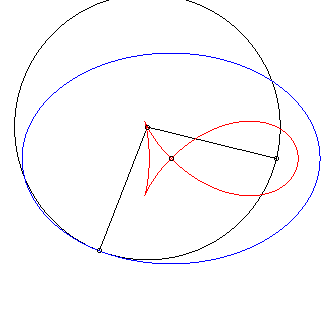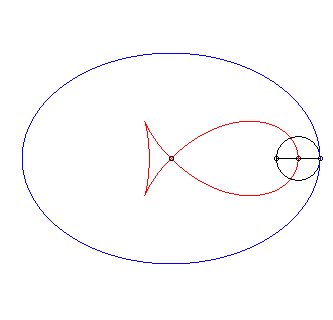 |
|
Second special case: negative pedal of the ellipse with respect to a major summit (d = a). The parametrization simplifies to: |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017