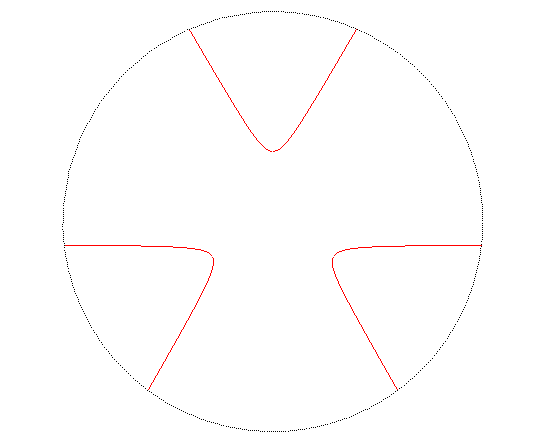
EQUILATERAL TREFOIL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
EQUILATERAL TREFOIL

| Curve studied by G.
de Longchamps in 1884.
Other name: Longchamps trisectrix. |
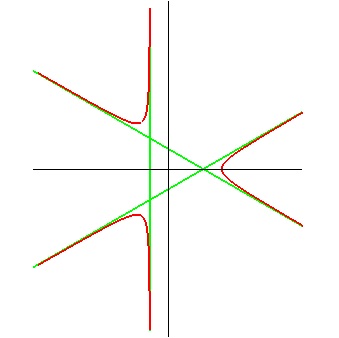
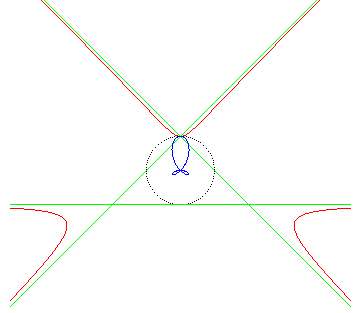
The asymptotes form an equilateral triangle. |
Polar equation: Cartesian equation: (nota: (0,0) is an isolated point of the algebraic curve). Cartesian parametrization: Rational cubic with an isolated point (O). |
The equilateral trefoil is:
- an epispiral with 3 branches
| - the inverse of the regular trifolium with respect to its centre
|
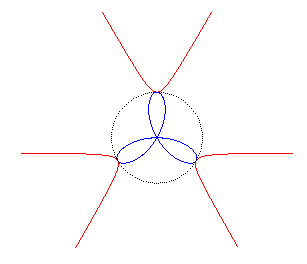 |
| - therefore, it is also the reciprocal polar of the negative pedal of the trifolium, namely, the deltoid | 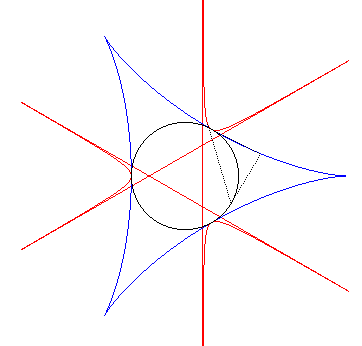 |
| - the curve obtained as the locus of the intersection points between two tangents at P and Q to a circle with centre O, the angle Explanation: the line (PQ) envelopes the deltoid, polar of the trefoil. |
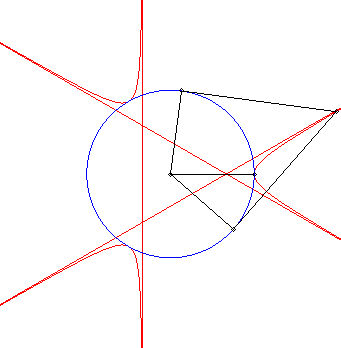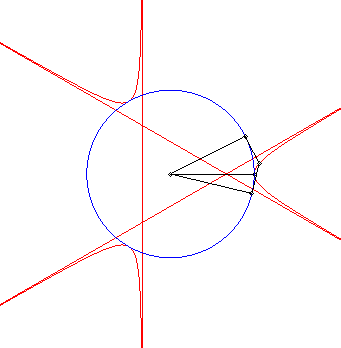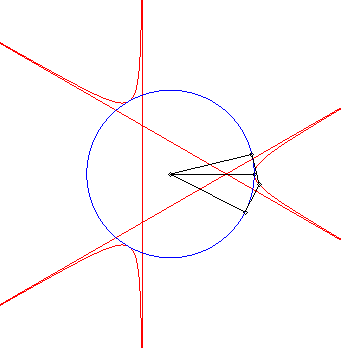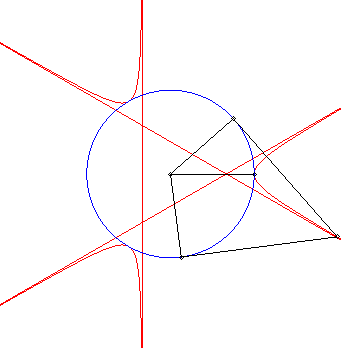 |
| - the planar section of a sinusoidal cone |
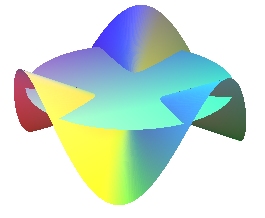 |
As indicated by its second name, it is a trisectrix.
|
This curve is quite close to the curve with polar equation |
 |
Ditto with the curve with polar equation 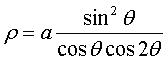 , Cartesian equation , Cartesian equation 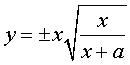 . . |
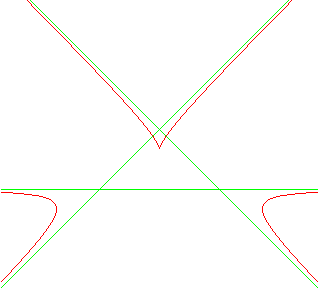 |
The equilateral trefoil and the Humbert cubic (similar shape, but the asymptotes of which intersect) are the only cubics with a rotation symmetry of order 3 (see Goursat curve).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017