Regular trifolium

REGULAR TRIFOLIUM

Curve studied by Longchamps in 1885, Brocard and d'Ocagne in 1887.
From the Latin trifolium "trefoil".

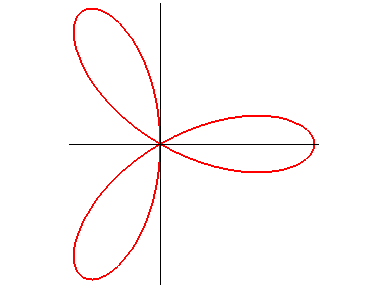Polar equation:

.
Cartesian equation:

.
Rational quartic.
Length:

.
Area:

(equal to the quarter of that of the circumscribed disk).

The regular trifolium is the rose with three petals.

It can be obtained as the trajectory of the second intersection point between a line and a circle turning around one of their points, either in the same direction and the circle four times as fast as the line, either in opposite directions and the circle turning twice as fast as the line.
It can also be obtained as the trajectory of the second intersection point between two identical circles turning around one of their points, in opposite direction, one of them turning twice as fast as the other.

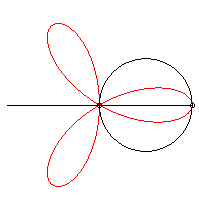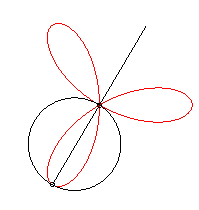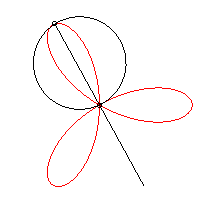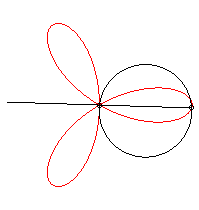Therefore, it is a hypotrochoid (base circle with radius , rolling circle with radius , distance from the point to the rolling circle = ),

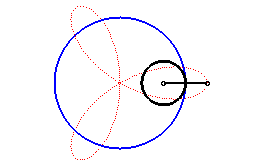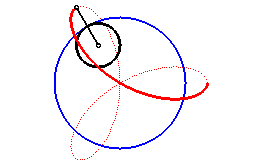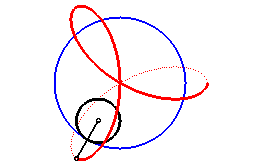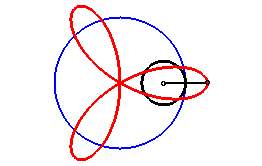
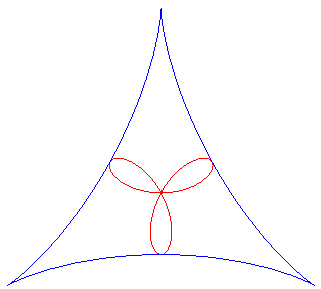
and the pedal of a deltoid with respect to its centre, like all trifolia.

It thus is also the envelope of a circle the diameter of which joins the centre of a deltoid to a point on this deltoid.

The regular trifolium can also by obtained by projections from a cylindric sine wave with 3 arches, through a 3D basin.

See here how to "thicken" a trifolium to a get triple torus.

See the trifolium on the Roman surface.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra