CEVA TRISECTRIX AND SECTRIX
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CEVA TRISECTRIX AND SECTRIX

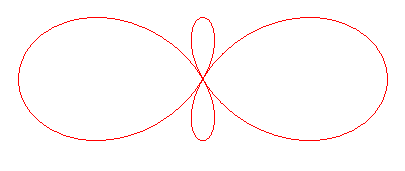
| Curve studied by Ceva in 1699.
Giovanni Ceva (1648-1734): Italian mathematician and engineer. |
| Polar equation: Cartesian parametrization: Complex parametrization: Cartesian equation: Rational sextic. |
| Given a circle (C) with centre O and radius a and a line (D) passing by O ((D) is here Ox), the Ceva trisectrix is the locus of the point M such that OP = PQ = QM with P on (C), Q on (D) and such that O, P and M are aligned.
The angle xOM is the third of the angle xQM, hence the name of trisectrix. Compare to the construction of the Maclaurin trisectrix. |
 |
|
|
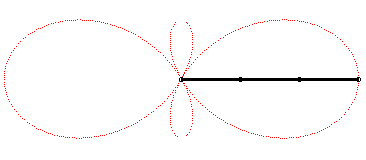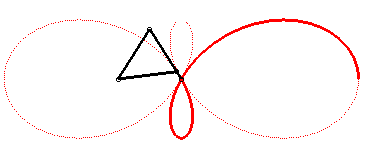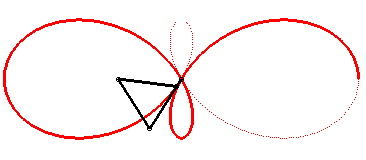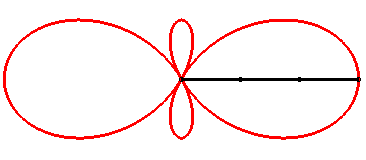 |
| Like all tritrochoid, the Ceva trisectrix is the locus of the gravity centre of 3 circular motions. |
 |
This curve is also a conchoid of the quatrefoil
(therefore, a conchoid of a rose).
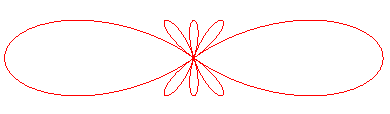
The construction above can be continued, as shown in the figure below:

| The curve of order n, with polar equation |
|
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017