Polar parametrization:   where ;  we have (see the figure below). Polar equation: . Polar equation when a = c : . Cartesian equation of  {0}: . Elliptic tricircularsextic.

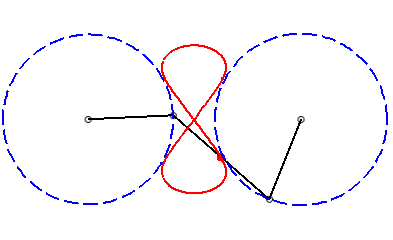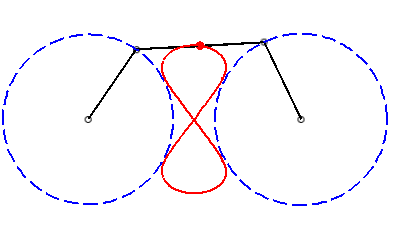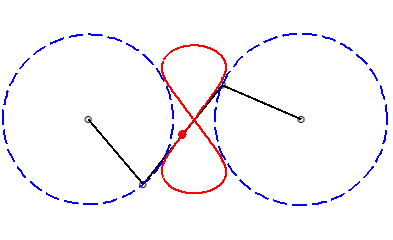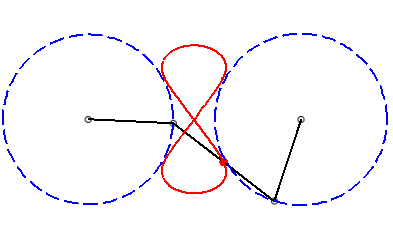
A Watt curve is the locus of the middle of the connecting rod [PQ] of an articulated quadrilateral (APQB) satisfying AP = BQ, A and B being fixed - it is therefore a special case of three-bar linkage curve where the cranks have equal lengths; here, A(0, a), B(0, –a), AP = BQ = b, PQ =2c.

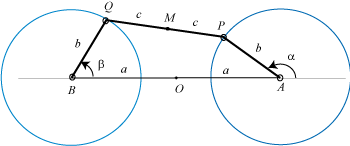
In other words, a Watt curve is the locus of the middle of a segment line with constant length joining two circles with same radii (the circles (C_A) and (C_B) with centres A and B and radii b), think of it, for example, as the middle of a rod connecting two wheels.

The curve is not empty iff  ./
 
 
 

The curve passes by O iff a, b, c are the lengths of the sides of a triangle, i.e. , i.e. ; then, the point O is, at the same time, double point and inflection point of each branch, which are almost linear in a neighbourhood of O. If we look for the points where the tangents at O recut the curves, we find that these points coincide with O (in other words, the contact is of order 2) when . Watt, who was trying to obtain a motion as linear as possible for his steam engine, designed his mechanism in this case, which is the most interesting one when the two bars AP and BQ are horizontal when M passes by O, and the bar QP is vertical. The interest of obtaining a linear motion by an articulated system is to avoid the friction due to the sliders, that imply greater wear.

Watt's mechanism: a = 5, b = 4, c= 3.

 

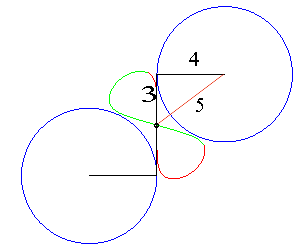
When the length of the connecting rod [PQ] is equal to that of the fixed bar [AB] (c = a), the curve is composed of the reunion of the circle (O, b) (case where (APQB) is a parallelogram), and a Booth curve; we get an oval if b > 2a, two circles if b = 2a (case where the quadrilateral is a square), a lemniscate if b < 2a, which is a lemniscate of Bernoulli when .
NB: in the animations below, P travels along (C_A) at constant speed, which creates jolts in the motion of Q on (C_B).

case a = c < b/2: Booth oval + circle

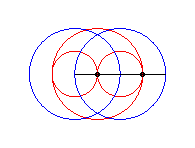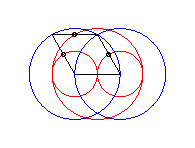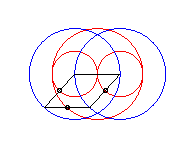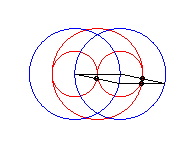
case a = c = b/2: three circles; for the two red small circles, the articulated quadrilateral is completely folded on itself

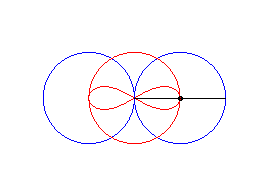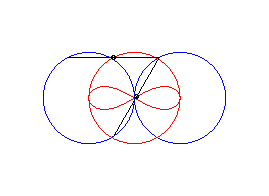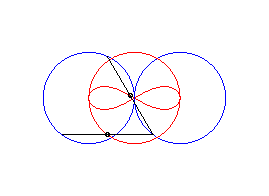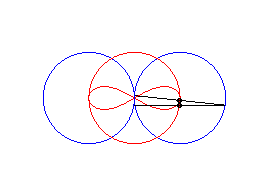
case a = c > b/2: lemniscate of Booth + circle

In a general fashion, the passage by O is obtained for , formula that also gives the polar angles of the corresponding tangents. Note that if d = 0, i.e. , then the tangents coincide.

In the case a ¹c, the curves therefore assume the following shapes:
 

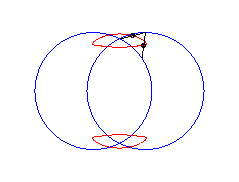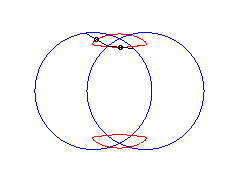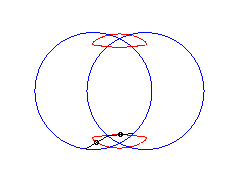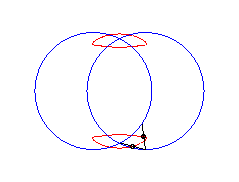
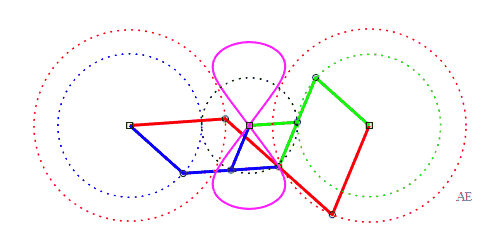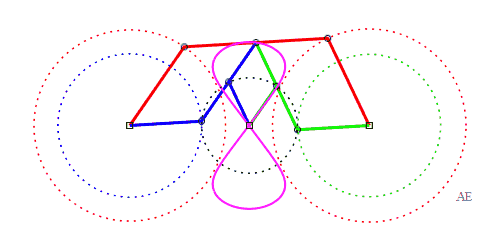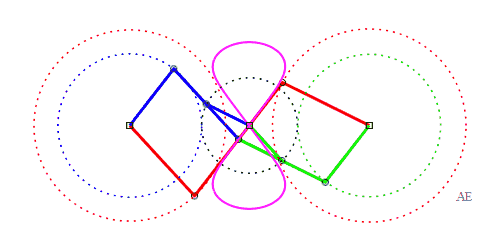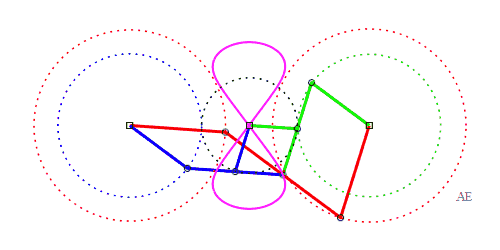
b > a + c et c < 2a:  curve with two components

:  curve with two crossings

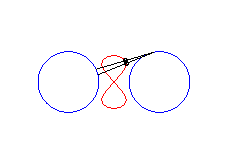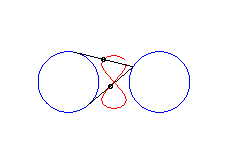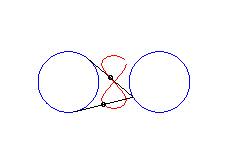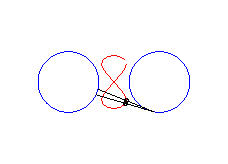
|a-b| < c < a: vertical eight

 

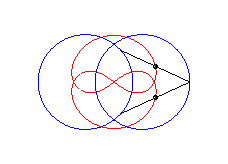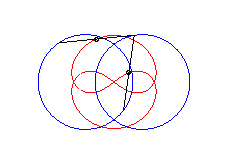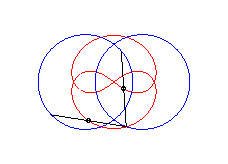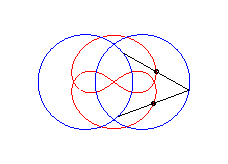
:  curve with three crossings.

: vertical eight with tangent crossing.

: vertical eight.

 

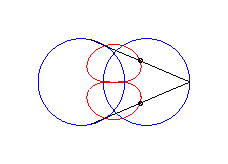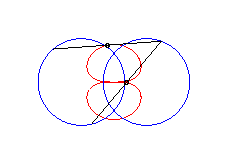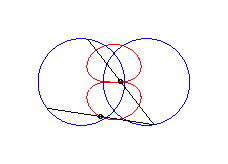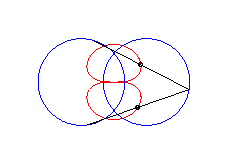
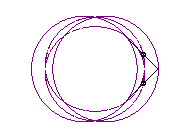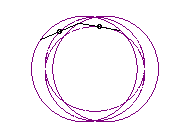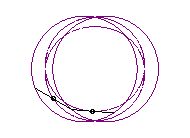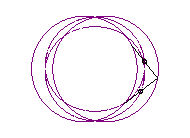
The principle of triple generation of the three-bar curves applies to the Watt curve. In the figure opposite, the point P' is such that AP'MP is a parallelogram, and Q" is such that BQMQ" is a parallelogram. The same curve is therefore obtained by the three-bars AP'Q'O and the three-bars OP"Q"B, but this time, Q' is the midpoint of [P'M], and P" is the midpoint of [Q"M].

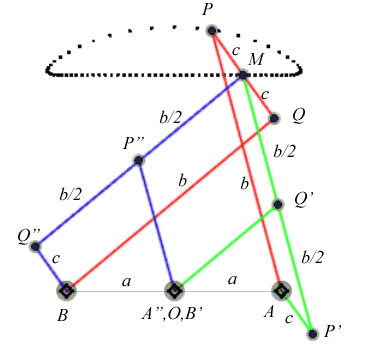In the case where the curve has two connected component, the 2 intersection points with the median symmetry axis have zero curvature if ; in the case a = 2 , c = 1 we have b = ; the approximation with a line is then far better than with the Watt mechanism.

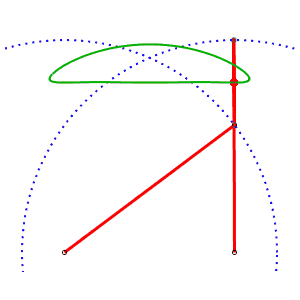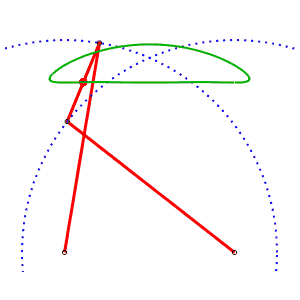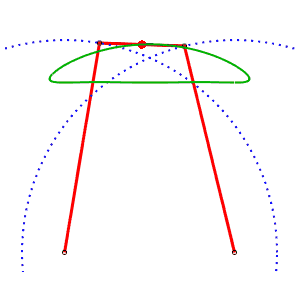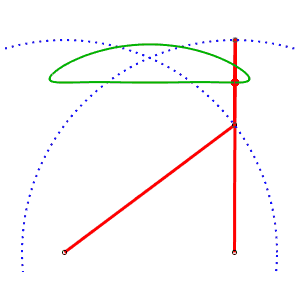
Chebyshev linkage AB= 4, AP=BQ= 5, PQ = 2, M midpoint of PQ

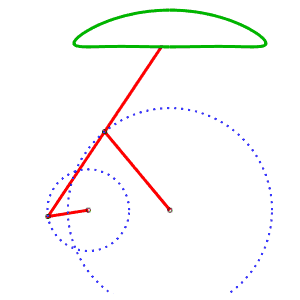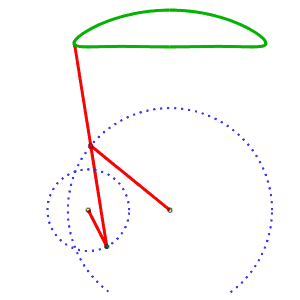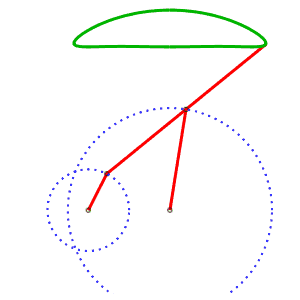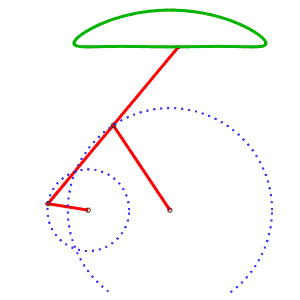
The alternative generation of the same curve allows to have a mechanism where the curves do not cross. AB = 4, AP = 5, BQ = 2, PQ = 5, P midpoint of QM

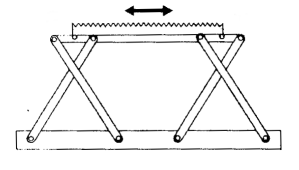
Saw using the Chebyshev linkage

But here is what becomes of the pseudo-linear part when the ordinates are elongated:

See also the Roberts mechanism at three-bar linkage curve.
 

A mathematically linear motion obtained by an articulated mechanism requires at least 5 moving bars, and it obtained, for example, with the Hart mechanism, or the Peaucellier linkage.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2021