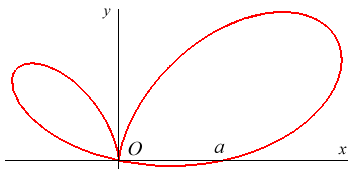Équation polaire :  . Équation cartésienne :  . Paramétrisation cartésienne rationnelle : . Quartique circulaire rationnelle.

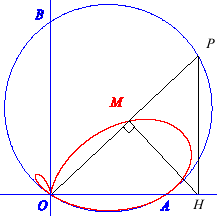
(C) étant le cercle passant par O, A(a, 0) et B(0, b), et une droite variable passant par O recoupant (C) en P, de projeté H sur Ox, le bifolium associé est le lieu du projeté M de H sur la droite (OP).
 
 

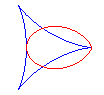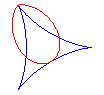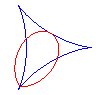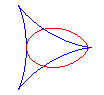
Les bifoliums sont les podaires de deltoïde par rapport à l'un de ses points (ici : O) ; voir les rapports entre le bifolium et la deltoïde à folium.

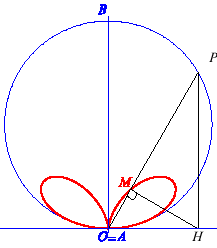
Lorsque a = 0, c'est-à-dire lorsque la podaire est prise par rapport à un point de rebroussement de la deltoïde, on obtient le bifolium régulier.
Lorsque b = 0, c'est-à-dire lorsque la podaire est prise par rapport à un sommet de la deltoïde, on obtient le folium simple.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2000