Problème posé et résolu par Jean Bernoulli en 1718, et étudié par Nathan Moscovitch en 1934. Autre nom : brachistochrone isopérimétrique.

 

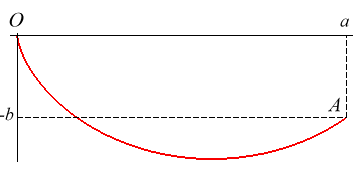
La brachistochrone de longueur donnée est la courbe de longueur l sur laquelle doit glisser sans frottement et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur uniforme de sorte que le temps de parcours soit minimal parmi toutes les courbes de longueur l joignant deux points O et A fixés (ici A(a, -b)).

 

Problème de départ :  minimale, pour  donnée. Équation différentielle (obtenue par application de l'équation d'Euler-Lagrange) : . (voir ici un peu plus de détails) Paramétrisation :  où  et  (pour k = 0, on retrouve la brachistochrone usuelle, autrement dit la cycloïde). Abscisse curviligne donnée par : . Temps de parcours  donné par : . Autre paramétrisation : .

 
 

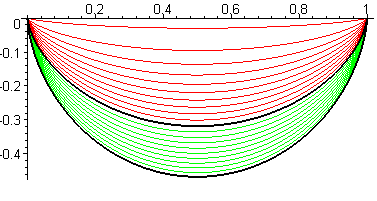
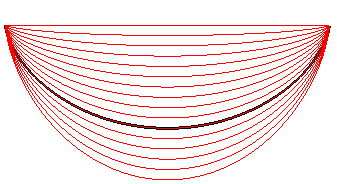
Vue des diverses brachistochrones joignant O = (0, 0) à A = (a, 0) pour k entre –1 et 1, et a = 1. Pour k tendant vers –1, la courbe limite est le segment [OA], de longueur a, temps de parcours infini. Pour k = 0, (limite rouge vert), on obtient la cycloïde de longueur , temps de parcours minimal . Pour k = 1 (courbe du bas), on obtient une courbe de longueur 5a/2 , temps de parcours (courbe rationnelle, comme l'avait remarqué Bernoulli). Relation entre c et a : . Longueur d'une arche complète : . Flèche de l'arche : . Temps de parcours : .

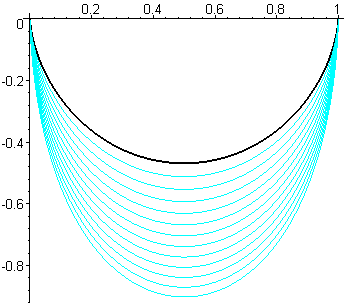
Vue des diverses brachistochrones joignant O = (0, 0) à A = (a, 0) pour k > 1 et a = 1. Relation entre c et a : . Longueur d'une arche complète : . Flèche de l'arche : . Temps de parcours : .

Remarque : ces courbes sont aussi solutions du problème dual : déterminer la courbe de temps de parcours donné ayant une longueur minimale.
 

Comparaison entre les courbes obtenues par l'équation différentielle, (à gauche) et de simples dilatations de la cycloïde (à droite) ....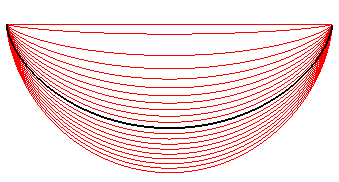

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2012