COURBE DE CATALAN
Catalan's
curve, catalansche Kurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE CATALAN
Catalan's
curve, catalansche Kurve

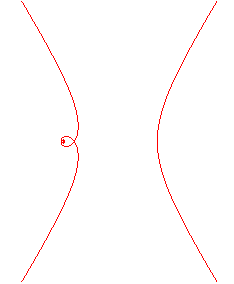
| Courbe étudiée par Catalan
en 1856, et par C.
Masurel en 2013.
Eugène Charles Catalan (1814-1894) : mathématicien franco-belge. |
 |
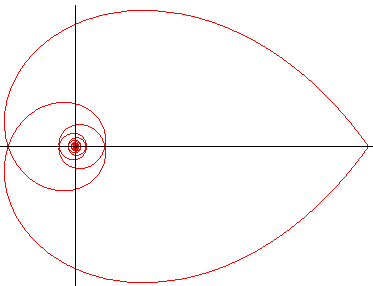 |
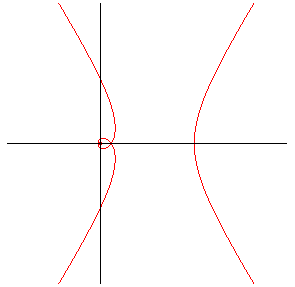
Équation polaire : Abscisse curviligne : Rayon de courbure : |
 |
La courbe de Catalan est la solution au problème
suivant : trouver la courbe qui, roulant sans glisser sur une droite D,
possède un point de son plan qui décrive un cercle tangent
à D.
En simplifié, la courbe de Catalan est solution du problème de la roulette circulaire. |
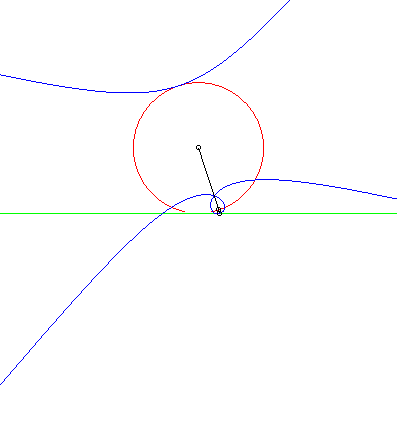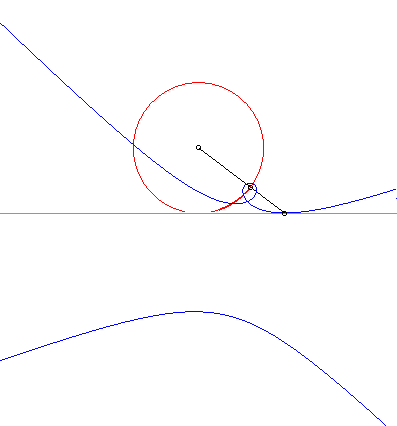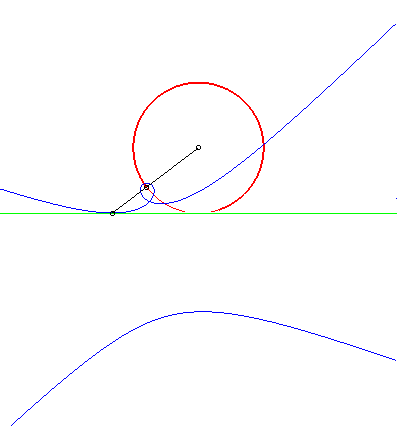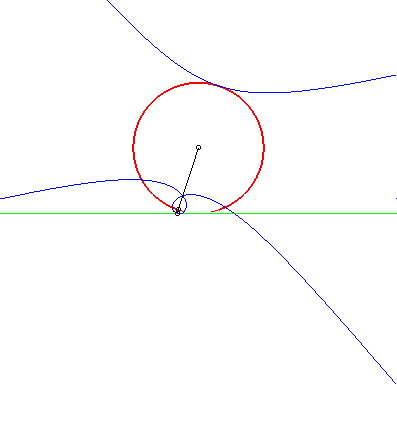 |
D'après le théorème affirmant que les glissettes à base rectiligne d'une courbe sont les roulettes à base rectiligne de la développée de cette courbe, la courbe de Catalan est la développée de la spirale tractrice (qui est, elle, solution du problème de la glissette circulaire).
Le calcul de l'abscisse curviligne montre que la courbe
de Catalan est une solution de l'équation ,
dont l'autre solution est le cercle.
L'équation polaire mise sous la forme
montre que c'est la médiane polairede
deux spirales hyperboliques.
Si l'on souhaite qu'un point du plan de la courbe roulante
décrive un cercle non tangent à la base, on obtient une courbe
roulante d'équation polaire
où a est le rayon du cercle et d la distance du centre
du cercle à la base.
C'est une polygastéroïde,
développée de tractoire de cercle.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2013