DÉVELOPPANTE D'UNE COURBE PLANE
Involute
of a plane curve, Evolvente einer ebenen Kurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
DÉVELOPPANTE D'UNE COURBE PLANE
Involute
of a plane curve, Evolvente einer ebenen Kurve

| Notion étudiée par le Marquis de l'Hospital en 1696, Fontenelle en 1712 (qui lui a donné son nom), puis par Cesaro en 1888. |
| Si M0 est le point
courant de Paramétrisation cartésienne : Paramétrisation complexe : Rayon de courbure : |
Les développantes d'une courbe plane
sont les courbes tracées par l'extrémité d'un fil
tendu le long de
et s'enroulant le long de
; autrement dit, ce sont les traces dans le plan d'un point d'une droite
pivotant sans glisser sur
(ce sont donc des cas particuliers de roulettes).
Ce sont donc aussi les trajectoires orthogonales de la famille des tangentes à la courbe, ou encore les courbes dont la courbe de départ est la développée.
Les développantes d'une courbe sont des courbes
parallèles
entre elles.
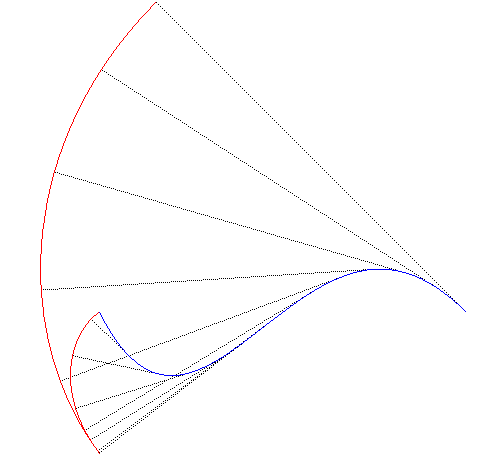
| On notera (cf. figures ci-dessus et ci-contre) qu'un
point d'inflexion de la courbe de départ donne naissance à
un point de rebroussement de deuxième espèce dans la développante,
comme l'avait déjà fait remarquer le Marquis de l'Hospital
en
1696 (voir
ce
texte).
Ci-contre, le point d'inflexion en A provoque le point de rebroussement de deuxième espèce en F. |
Exemples : (voir aussi à développée)
| courbe de départ | origine | développante, ou l'une d'entre elles |
| cercle | quelconque | développante de cercle ! |
| point | quelconque | cercle |
| cycloïde | sommet | la même cycloïde translatée |
| cardioïde | sommet | cardioïde semblable dans le rapport 3 |
| néphroïde | sommet | néphroïde semblable dans le rapport 2 |
| néphroïde | point de rebroussement | sextique de Cayley |
| épicycloïde de paramètre q | sommet | épicycloïde semblable dans le rapport (q + 2)/q |
| deltoïde | sommet | deltoïde semblable dans le rapport 1/3 |
| astroïde | sommet | astroïde semblable dans le rapport 1/2, croix de Malte |
| hypocycloïde de paramètre q | sommet | hypocycloïde semblable dans le rapport (q-2)/q |
| spirale logarithmique |
centre | spirale logarithmique |
| chaînette | sommet | tractrice |
| parabole | sommet | développante sommitale de parabole |
| logarithmique | quelconque | développante d'exponentielle |
| développante de cercle | point de rebroussement | spirale de Norwich |
Voir la généralisation
aux courbes 3D, ainsi que la généralisation
aux développantes obliques.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023