Courbe de Holditch

COURBE DE HOLDITCH
Holditch curve, holditchsche Kurve

Courbe étudiée par Holditch en 1858, H. Benitez en 1980, et Monterde & Rochera en 2017.
Animations ci-dessous réalisés par Alain Esculier.

Pour obtenir la courbe de Holditch de , d'équation f(x, y) = 0 : éliminer entre les équations, avec .

Les courbes de Holditch associée à une courbe donnée sont les lieux des points M fixés d'une droite dont deux points fixés A, B, appartiennent à . Holditch a considéré ces courbes car lorsque est fermée, et sous certaines conditions, il a démontré que la différence entre l'aire enserrée par et celle enserrée par la courbe de Holditch vaut ,où (voir le théorème de Holditch).
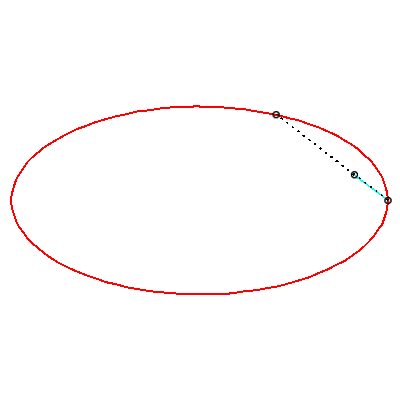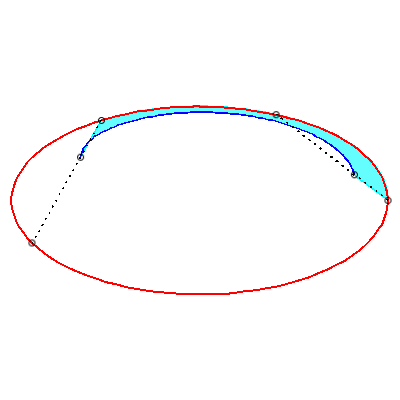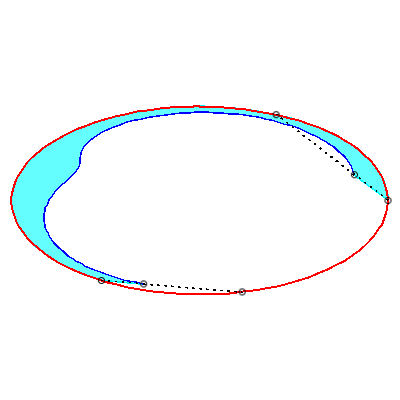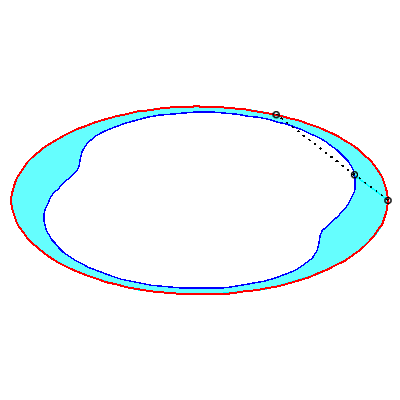Ces courbes sont des cas de glissettes, les deux point A et B "glissant" sur la courbe (voir le cas particulier numéro 2 dans la page sur les glissettes).

L'obtention de l'équation de la courbe de Holditch est en général difficile, mais voici deux cas simples :

Pour une ellipse:, avec une corde de longueur 2c, le point traceur étant situé au centre, la courbe de Holditch a pour équation cartésienne : (quartique de genre 2).
Équation polaire : .
Pour une hyperbole, changer le signe devant y².
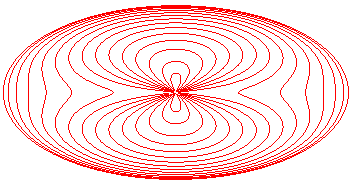
Perte de convexité pour c > p = b²/a.

Pour une parabole:, la courbe de Holditch, pour une corde de longueur 2c, le point traceur étant situé au centre, a pour équation cartésienne : (quartique).
Perte de convexité pour c > p .

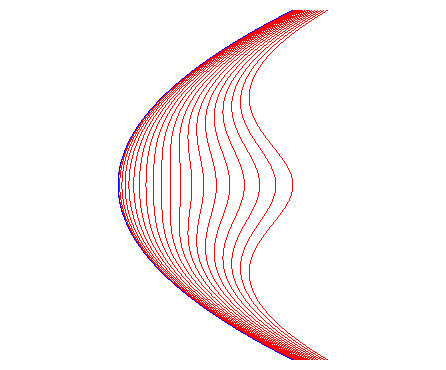Voici l'évolution de la courbe de Holdich complète de l'ellipse, pour un point traceur situé entre A et B, hors du centre, corde de longueur 2c. Pour , elle est formée de deux courbes continues symétriques par rapport aux axes de l'ellipse.
Chacune de ces courbes est...

convexe pour ,

fermée sans point double, parcourue d'un mouvement sans rétrogradation, où la corde revient à son point de départ après avoir fait un tour complet, pour ,

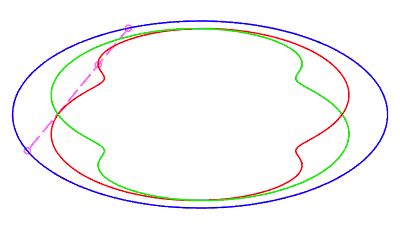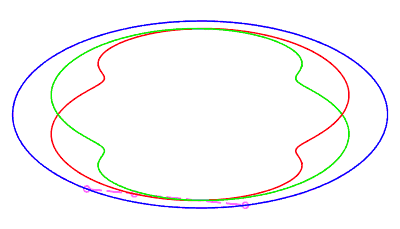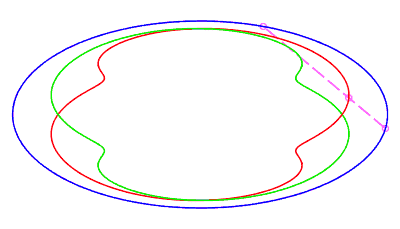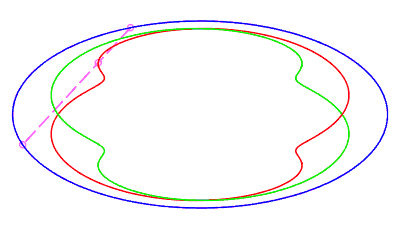fermée sans point double, parcourue d'un mouvement avec phase rétrograde, où la corde revient à son point de départ après avoir fait un tour complet, pour
.
Le nombre d est la demi longueur minimale d'une corde dont une extrémité est perpendiculaire à l'ellipse (instant terminant la phase de rétrogradation, cf. l'animation ci-contre).

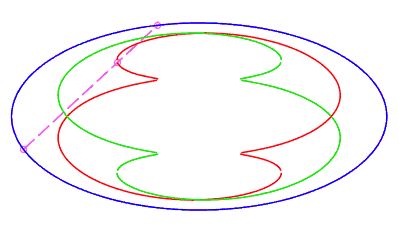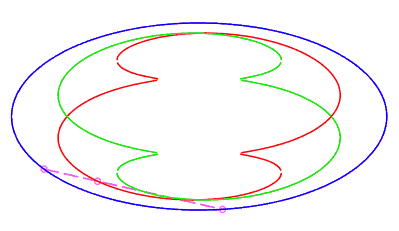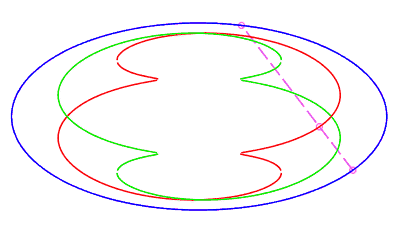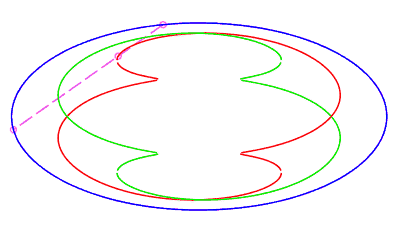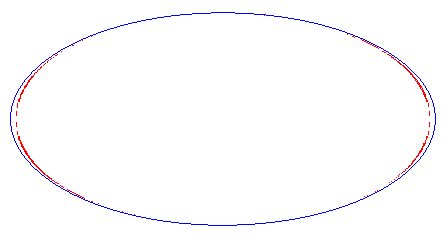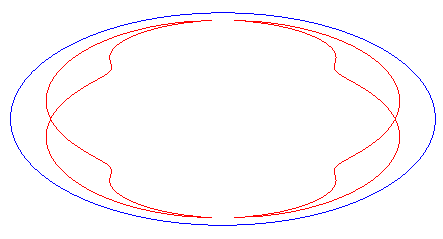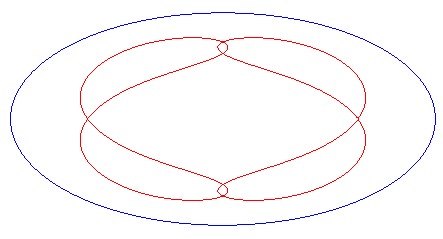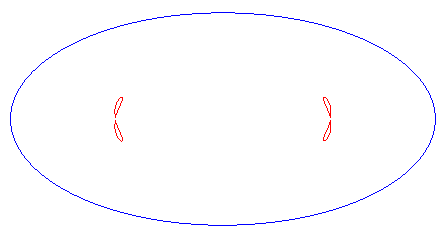
en forme de huit, parcourue par un mouvement avec rétrogradation où la corde revient à son point de départ sans rotation, pour b < c < a.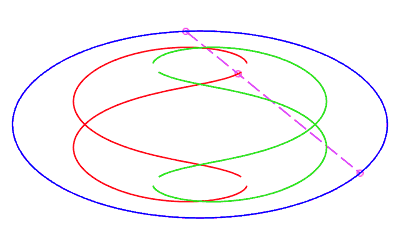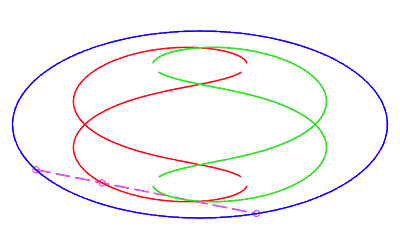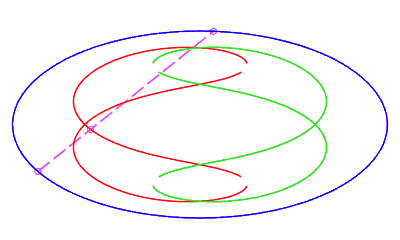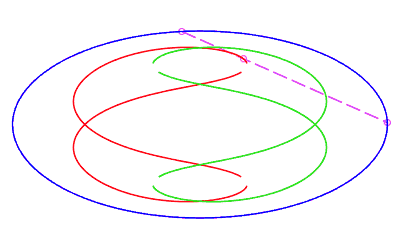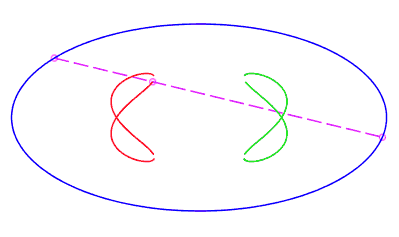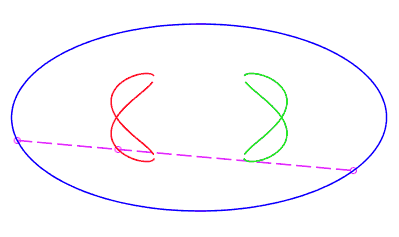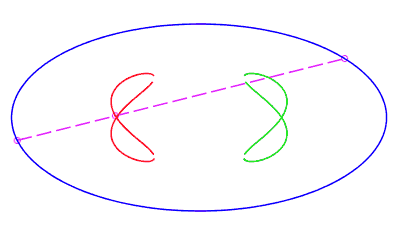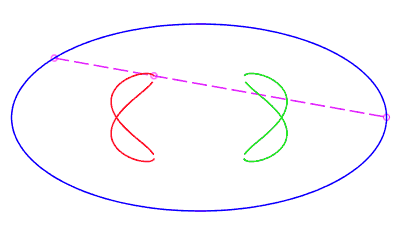

Animation de la déformation de la courbe complète pour 0 < c < a.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Pour une ellipse:, avec une corde de longueur 2c, le point traceur étant situé au centre, la courbe de Holditch a pour équation cartésienne : (quartique de genre 2). Équation polaire : . Pour une hyperbole, changer le signe devant y².	Perte de convexité pour c > p = b²/a.
Pour une parabole:, la courbe de Holditch, pour une corde de longueur 2c, le point traceur étant situé au centre, a pour équation cartésienne : (quartique). Perte de convexité pour c > p .

convexe pour ,
fermée sans point double, parcourue d'un mouvement sans rétrogradation, où la corde revient à son point de départ après avoir fait un tour complet, pour ,
fermée sans point double, parcourue d'un mouvement avec phase rétrograde, où la corde revient à son point de départ après avoir fait un tour complet, pour . Le nombre d est la demi longueur minimale d'une corde dont une extrémité est perpendiculaire à l'ellipse (instant terminant la phase de rétrogradation, cf. l'animation ci-contre).
en forme de huit, parcourue par un mouvement avec rétrogradation où la corde revient à son point de départ sans rotation, pour b < c < a.
Animation de la déformation de la courbe complète pour 0 < c < a.