Notion étudiée par Newton.

 

	équation cartésienne	paramétrisation cartésienne
courbe de départ
hyperbolisme par rapport à O et la droite x = a
antihyperbolisme

 

L'hyperbolisme d'une courbe  par rapport à un point O et une droite (D) est la courbe  lieu du point M défini comme suit : (M0) étant un point de , la droite (OM0) coupe (D) en P ; M est le projeté de P sur la parallèle à (D) passant par M0. Analytiquement, la droite (D) étant x = a, la transformation de  vers  s'écrit; elle est quadratique, donc transforme une courbe algébrique de degré n en une courbe algébrique de degré  2n.

Pour la transformation inverse : , on parle d'antihyperbolisme.
Exemples :
 

antihyperbolisme	O et (D)  (pour la courbe de départ)	O et (D)  (pour la courbe d'arrivée)	hyperbolisme
cercle	O sur le cercle, (D)   tangente au cercle opposée à O	O au "milieu" de l'asymptote et (D)  tangente sommitale	cubique d'Agnesi
cercle	O centre du cercle, (D) tangente au cercle	O au centre et (D) tangente sommitale	quartique de Külp
cercle	(D) perpendiculaire à la droite joignant O au centre du cercle (cas englobant les précédents)		Oeuf de Granville
cercle	O sur le cercle, (D)  parallèle au diamètre passant par O	O au centre et (D) passant par les points d'intersection avec le cercle	anguinée
lemniscate de Gérono :  (à une affinité près)	O au centre, (D) tangente à un sommet	O au centre, (D) tangente au cercle	cercle
quartique piriforme	O au rebroussement, (D) perpendiculaire à l'axe de symétrie	O sur le cercle, (D)  parallèle à la tangente au cercle en ce point	cercle
parabole divergente rationnelle :	O au centre, (D) : x = a	O au centre et (D) : x = a	parabole :
parabole cubique :	O et droite x = a	O et droite x = a	trident :
visiera :	O et droite x = a	O et droite x = a	versiera :

Si l'on remplace la droite (D) par une courbe quelconque, on obtient plus généralement la transformation de Newton :
 

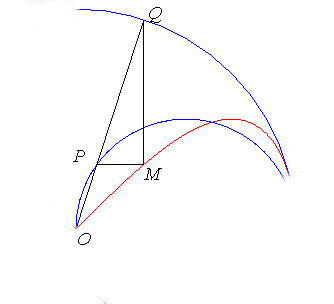La transformée de Newton d'un couple de courbes (, ) par rapport à un repère Oxy  est la courbe  lieu du point M défini comme suit : une droite (D) passant par O coupe  en P et  en Q ; M est le point d'intersection de la parallèle à Ox passant par P et de la parallèle à Oy passant par Q. On retrouve l'hyperbolisme en prenant pour une droite parallèle à Oy.

 

Paramétrisation cartésienne de la transformée de Newton des courbes  et  par rapport à Oxy : .

Exemples :
 

première courbe (G1)	deuxième courbe (G2)	transformée
cercle de centre O	cercle de centre O	ellipse (obtenue par "réduction d'ordonnée")
cercle centré sur Ox passant par O	cercle de centre O	courbe en huit , dilatée d'une lemniscate de Gerono (non dilatée quand a = b, soit quand les cercles sont tangents).
échange des cercles précédents		arc de parabole
cercle centré sur Ox	cercle de centre O	oeuf de Hügelschäffer

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2009