Courbe étudiée par Klein en 1879 (Uber die Transformationen siebenter Ordnung der elliptischen Funktionen, Math. Ann. 14 (1879), 428-471. Œuvres, Tome III, p. 90-136). Félix Klein (1849-1925) : mathématicien allemand. Webographie : en.wikipedia.org/wiki/Klein_quartic mathworld.wolfram.com/KleinQuartic.html math.univ-lyon1.fr/~germoni/memoires/stage_Le.pdf

1) La quartique affine de Klein :

Équation cartésienne :  où  de sorte que pqr = 0 est la réunion de 3 droites formant un triangle équilatéral centré en O. Quartique de genre 3. Équation polaire : . REM 1 : la quartique passe par les trois points d'intersection du cercle  avec les 3 droites précédentes et est tangente (doublement) à ces 3 droites en ces 3 points. REM 2 : c'est une courbe de Goursat. Comparer avec la définition de la surface de Kummer.

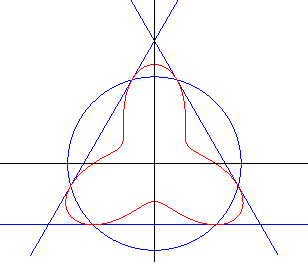
Cas , avec illustration de la remarque 1.

La même courbe, représentée avec sa hessienne, coupant la courbe en ses points d'inflexion. Lorsque , ce qui est le cas ici, les tangentes aux points d'inflexion sont paralèles à un axe de symétrie.

 
 

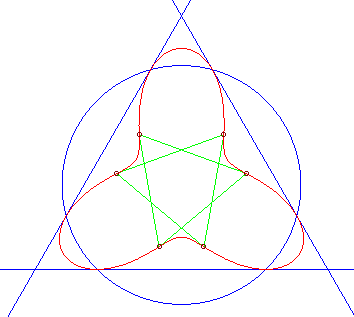
La quartique de Klein (affine) est la courbe ci-dessus dans le cas particulier où . Elle a la particularité que les tangentes aux 6 points d'inflexion (en vert ci-contre) passent par un autre point d'inflexion et forment deux triangles équilatéraux. Comparer avec la quartique de Loriga (qui a la même propriété, mais qui est différente).

2) La quartique projective de Klein (projectivement équivalente à la précédente) :
 

Équation homogène :

 

Vues du cône: (que l'on peut désigner par "cône de Klein") coupé par le plan , donnant une réalisation affine de la quartique projective de Klein (différente de celle du 1)). L'équation cylindrique de ce cône dans un repère où Oz est l'axe de rotation est : .

Cône de Klein, par Alain Esculier

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2014