Limaçon de Pascal

LIMAÇON DE PASCAL
Limaçon (or snail) of Pascal, Pascalsche Schnecke
cercle, limaçon à boucle, cardioïde, limaçon haricot, et 2 limaçons convexes

Courbe étudiée par Dürer en 1525 (sous le nom d'arachnée), Étienne Pascal en 1630, et Roberval (qui a donné le nom à la courbe) en 1650.
Étienne Pascal (1588 -1651) : magistrat et mathématicien amateur, père de Blaise.

Équation polaire :

(a, e > 0) .
Paramétrisation complexe :

(

).
Équation cartésienne :

(voir ici un article sur une courbe proche, d'équation

).
Quartique bicirculaire rationnelle (point singulier en O).
Aire pour e1 :

(voir le théorème de Holditch).

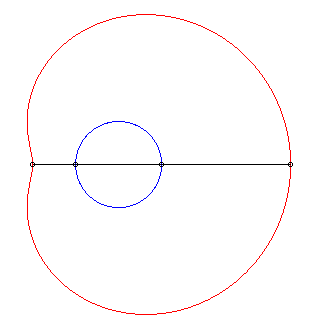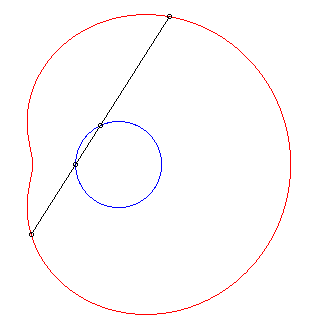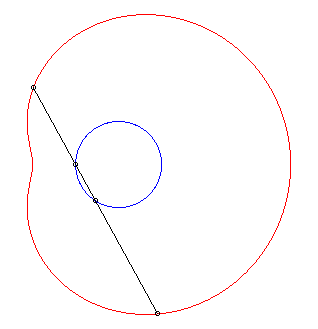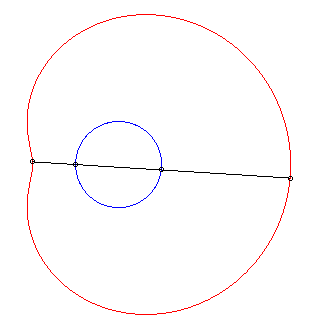
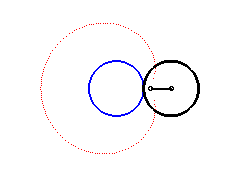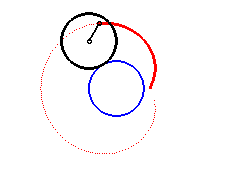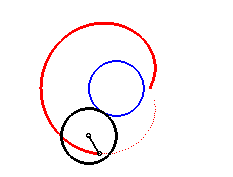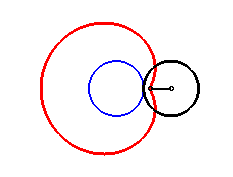
Les limaçons de Pascal sont les conchoïdes d'un cercle relativement à l'un de ses points O (ici, le cercle est de diamètre [OA] avec A(ea, 0), le module de la conchoïde étant a).

D'où la construction mécanique suggérée ci-contre, à partir d'un bâton de longueur 2a coulissant par un point d'un cercle de diamètre ea et dont le milieu est astreint à parcourir le cercle.

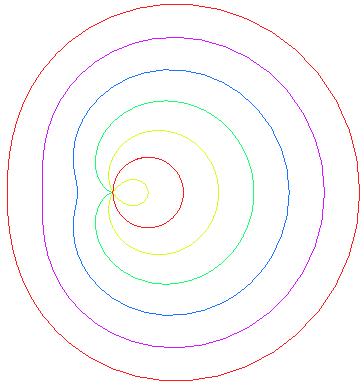
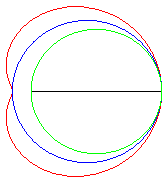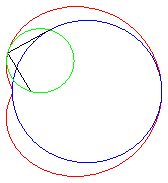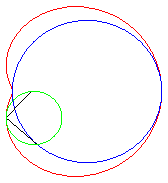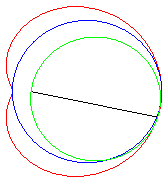
Les courbes prennent différentes formes suivant les cas :

e < 1: limaçon elliptique (inverse d’une ellipse par rapport à son foyer), ou à point isolé, ou acnodal ;
     .e < 1/2 : courbe convexe qui "tend" vers le cercle C(O, a) quand e tend vers 0
     .e = 1/2 : limaçon de Pascal à méplat.
      .1/2 < e < 1 : courbe en forme de haricot ;
e = 1 : limaçon cuspidal plus communément appelé cardioïde.
e > 1 : limaçon hyperbolique (inverse d’une hyperbole par rapport à son foyer) ou à boucle, ou crunodal ; c'est une courbe fermée avec boucle ; pour e = 2, on obtient le limaçon trisecteur, qui est aussi une rosace.
cercle, limaçon à boucle, cardioïde, limaçon haricot, et 2 limaçons convexes

La paramétrisation complexe ci-dessus montre que les limaçons de Pascal sont les épitrochoïdes engendrées par un point lié à un cercle roulant sans glisser autour d’un cercle de même rayon (ici le cercle fixe est le cercle de diamètre [OA] et le point traceur est situé à une distance a du centre du cercle mobile).

Ce sont aussi, comme toute quartique bicirculaire rationnelle :
- les podaires de cercle (ici podaire du cercle de centre A et de rayon a par rapport à O).

Ce sont donc les enveloppes de cercle de diamètre d'extrémités un point fixe (ici, O) et un point d'un cercle (ici, du cercle de centre A et de rayon a).

- les inverses de coniques par rapport à l’un de leurs foyers (ici, de la conique d’excentricité e :

par rapport à O).

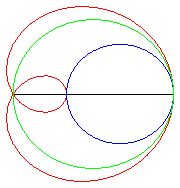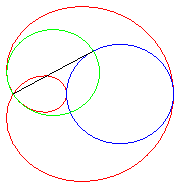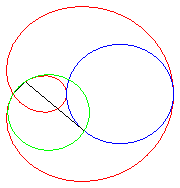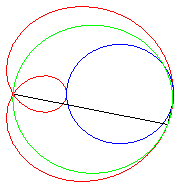- les cissoïdales de deux cercles dont l'un passe par le centre de l'autre, par rapport à ce centre (ici cissoïdale par rapport à O du cercle de centre (-ea/2, 0) passant par O et du cercle de centre O et de rayon a - cette définition est en fait équivalente à la définition conchoïdale).

Les limaçons de Pascal sont les cartésiennes rationnelles et sont des cas particuliers d'ovales de Descartes complets ; lorsque e1 (c'est-à-dire lorsque ce n'est pas une cardioïde), l'équation bifocale par rapport à O et O'( , 0) est : .

Plus précisément :
- le limaçon hyperbolique est la réunion des deux ovales de Descartes : (grande boucle) et (petite boucle).
- le limaçon elliptique est l’ovale de Descartes : (plus le point isolé O).

On retrouve aussi les limaçons de Pascal dans le système Bélidor de pont-levis.

Les développées des limaçons sont les caustiques par réflexion de cercle (source lumineuse à distance finie).

Les arachnées...

Les courbes d'équation (cissoïdales de cercle passant par O et rosace) offfrent un élégant remplissage du limaçon ; ici, k = 55/37 (idée de Thierry LEGAY) .

Voir ici un engrenage en limaçon de Pascal, et dans ce site une application technique à la montre "24 heures".

Voir aussi les conchoïdes de cercles générales.

Image réalisée par Daniel Alexis

Logo Nippon Telegraph and Telephone

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres